СП 128.13330.2016 Алюминиевые конструкции Актуализированная редакция СНиП 2.03.06-85 стр. 20

  1. Документы
  2. Своды правил (СП)
а - сумма высоты вертикальной полки поясного уголка с толщиной пакета горизонтальных листов;
t - суммарная толщина стенки и вертикальных полок поясных уголков.
Значение коэффициента φb в формуле (22) следует принимать:
при φ10,667  φb=φ1;
при φ1>0,667  φb=0,5+0,25φ1 , для алюминия всех марок, указанных в таблице 1, за исключением АМг3Н2, АД31T1 и АД31Т5, и φb=φ1, но не более 1,0 - для алюминия марок АМг3H2, АД31T1 и АД31Т5.
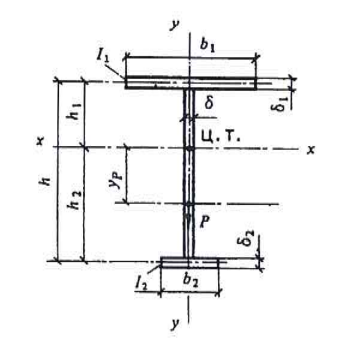
Д.4 Для разрезной балки двутаврового сечения с одной осью симметрии (рисунок Д.1) для определения коэффициента φb необходимо вычислить коэффициенты φ1 и φ2 по формулам:
241 × 61 пикс.     Открыть в новом окне
(Д.4)
269 × 62 пикс.     Открыть в новом окне
(Д.5)
383 × 51 пикс.     Открыть в новом окне
(Д.6)
В формулах (Д.4) - (Д.6):
ζ - коэффициент, зависящий от вида нагрузки и принимаемый по таблице Д.4;
h1, h2 - размеры, указанные на рисунке Д.1;
 - относительная координата точки приложения нагрузки со своим знаком (см. рисунок Д.1);
299 × 69 пикс.     Открыть в новом окне
здесь   (где I1, I2 - моменты инерции соответственно сжатого и растянутого поясов относительно оси симметрии сечения);
244 × 61 пикс.     Открыть в новом окне
It - момент инерции при кручении [см. обозначения к формуле (Д2)].
Значение коэффициента φb в формуле (22) следует принимать:
при φ10,667  φb=φ1;;
при φ1>0,667  φb=φ1 для алюминия всех марок, указанных в таблице 1, за исключением АМг3Н2, АД31Т1 и АД31Т5, для которых φ2 следует вычислять по формуле (Д.5) и принимать не более 1,0.
Таблица Д.1 - Коэффициент ψ для балок двутаврового сечения с двумя осями симметрии
Коэффициент α
Коэффициенты ψ
для балок без закрепления в пролете
при наличии не менее двух промежуточных закреплений верхнего пояса, делящих пролет на равные части, независимо от места приложения нагрузки
при сосредоточенной нагрузке, приложенной к поясу
при равномерно распределенной нагрузке, приложенной к поясу
верхнему
нижнему
верхнему
нижнему
1
2
3
4
5
6
0,1
0,98
2,80
0,91
2,14
1,20
0,4
0,98
2,84
0,91
2,14
1,23
1,0
1,05
2,87
0,95
2,17
1,26
4,0
1,26
3,05
1,12
2,35
1,44
8,0
1,47
3,29
1,30
2,56
1,65
16,0
1,89
3,75
1,68
2,94
1,96
24,0
2,24
4,10
2,00
3,22
2,24
32,0
2,56
4,45
2,28
3,50
2,49
48,0
3,15
4,97
2,73
3,99
2,91
64,0
3,64
5,50
3,15
4,45
3,33
80,0
4,10
5,95
3,50
4,80
3,64
96,0
4,48
6,30
3,89
5,15
3,96
128,0
5,25
7,04
4,48
5,78
4,50
160,0
5,92
7,77
5,04
6,30
5,01
240,0
7,35
9,17
6,30
7,56
6,09
320,0
8,54
10,40
7,32
8,40
7,00
400,0
9,63
11,48
8,16
9,38
7,77
Таблица Д.2 - Коэффициент ψ для балок двутаврового сечения с двумя осями симметрии при одном закреплении балки в середине пролета
Вид нагрузки
Место приложения нагрузки
Коэффициент ψ
Сосредоточенная
В середине пролета (независимо от уровня приложения)
Ψ=1,75 ψ1
Сосредоточенная
В четверти пролета к верхнему поясу
Ψ=1,14 ψ1
Равномерно распределенная
К верхнему поясу
Сосредоточенная
В четверти пролета к нижнему поясу
Ψ=1,6 ψ1
Равномерно распределенная
К нижнему поясу
Ψ=1,3 ψ1
Примечание - Здесь значение ψ1 следует принимать по графе 6 таблицы Д.1.
Таблица Д.3 - Коэффициент ψ для консолей двутаврового сечения с двумя осями симметрии
Коэффициент α
Коэффициент ψ при нагрузке, приложенной к поясу
верхнему
нижнему
4
0,875
3,640
6
1,120
3,745
8
1,295
3,850
10
1,505
3,920
12
1,680
4,025
14
1,855
4,130
16
2,030
4,200
24
2,520
4,550
32
2,975
4,830
40
3,290
5,040
100
5,040
6,720
Таблица Д.4 - Коэффициент ζ для балок двутаврового сечения с одной осью симметрии
Вид нагрузки
Чистый изгиб
Равномерно распределенная
Сосредоточенная сила в середине пролета
Момент на одном конце балки
Коэффициент ζ
1,00
1,12
1,35
1,75
346 × 340 пикс.     Открыть в новом окне
Рисунок Д.1 – Схема двутаврового сечения с одной осью симметрии
Д.5 Устойчивость балок швеллерного сечения следует проверять так же, как балок двутаврового сечения, при этом α вычислять по формуле (Д.2); найденные значения φb умножать на 0,7.
Значения Ix, Iy и It в формулах (Д.1) и (Д.2) следует принимать для швеллера.

Приложение Е Расчет внецентренно сжатых и сжато-изгибаемых элементов

Таблица Е.1 - Коэффициенты устойчивости φe для проверки устойчивости внецентренно сжатых (сжато-изгибаемых) сплошностенчатых стержней в плоскости действия момента, совпадающей с плоскостью симметрии
Условная гибкость 
Значение φe при приведенном относительном эксцентриситете mef
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
1,0
1,2
1,5
0,5
990
980
973
937
905
880
850
920
767
725
657
1,0
947
907
872
837
807
778
752
725
680
637
583
1,5
880
832
793
758
726
700
507
647
607
570
518
2,0
817
765
723
687
656
627
457
580
540
507
463
2,5
750
695
652
617
587
560
410
515
482
452
413
3,0
677
618
578
545
517
495
472
455
425
400
367
3,5
593
542
505
475
453
434
415
398
374
355
325
4,0
505
436
435
412
393
378
362
350
327
312
288
4,5
425
395
374
356
342
328
315
306
288
275
255
5,0
358
338
320
307
295
285
275
268
253
242
227
5,5
303
287
276
265
257
248
242
235
225
215
202
6,0
257
246
238
230
223
218
213
208
198
192
180
6,5
222
212
207
202
197
191
187
183
175
170
161
7,0
192
187
181
177
172
168
165
161
155
150
145
8,0
148
145
142
139
137
134
132
129
126
123
120
9,0
120
117
115
113
111
110
108
107
105
102
100
10,0
097
095
093
092
091
090
088
087
085
084
082
Окончание таблицы Е.1
Условная гибкость 
Значение φe при приведенном относительном эксцентриситете mef
2,0
2,5
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
0,5
567
500
445
360
302
257
225
203
182
165
1,0
505
445
394
323
272
235
205
186
167
151
1,5
452
398
355
292
247
215
188
171
153
140
2,0
405
358
320
265
227
197
175
158
142
130
2,5
362
322
290
242
208
182
162
146
132
121
3,0
323
290
262
220
192
167
150
135
123
114
3,5
288
260
236
202
175
155
140
126
116
108
4,0
257
233
214
184
159
144
130
117
109
101
4,5
230
210
193
167
146
132
121
110
102
095
5,0
205
190
175
152
135
123
113
103
096
090
5,5
185
172
160
140
125
115
105
097
090
085
6,0
166
155
145
128
115
106
097
090
085
080
6,5
148
141
132
117
107
097
090
085
080
075
7,0
135
128
120
108
098
090
085
080
075
070
8,0
112
107
100
091
085
080
077
072
067
062
9,0
094
090
086
080
076
072
067
063
059
055
10,0
080
077
075
070
067
062
060
056
052
048
Примечания
1 Значения коэффициентов φe в таблице увеличены в 1000 раз.
2 Значения φe  следует принимать не более значений φ.
Таблица Е.2 - Коэффициенты устойчивости φe  для проверки устойчивости внецентренно сжатых (сжато-изгибаемых) сквозных стержней в плоскости действия момента, совпадающей с плоскостью симметрии
Условная гибкость 
Значение φe при приведенном относительном эксцентриситете mef
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
1,0
1,2
1,5
0,5
950
888
825
755
718
660
635
605
540
495
436
1,0
882
810
756
693
660
609
582
548
496
453
405
1,5
872
753
684
643
607
568
534
507
458
420
375
2,0
773
700
640
593
558
523
492
468
423
390
347
2,5
712
637
585
543
508
477
450
427
390
358
320
3,0
640
575
530
488
458
430
408
387
355
327
294
3,5
565
507
467
432
410
385
365
350
321
297
270
4,0
490
442
410
382
363
343
327
313
290
269
247
4,5
418
382
357
335
320
304
290
280
260
243
223
5,0
353
328
309
293
280
268
257
249
233
219
202
5,5
300
282
267
256
245
237
228
222
208
197
183
6,0
256
242
233
223
216
210
202
197
187
178
166
6,5
220
210
205
197
190
185
182
175
167
160
150
7,0
192
186
180
173
169
165
162
157
150
145
136
8,0
150
145
142
139
135
133
130
127
122
120
112
9,0
120
117
115
112
110
108
107
105
101
098
095
10,0
097
096
095
093
092
091
090
087
085
083
082
Окончание таблицы Е.2
Условная гибкость 
Значение φe при приведенном относительном эксцентриситете mef
2,0
2,5
3,0
4,0
5,0
6,0
7,0
8,0
9,0
10,0
0,5
370
320
282
323
196
170
157
143
122
110
1,0
342
296
262
213
182
155
145
130
113
096
1,5
318
275
243
198
170
144
134
120
105
090
2,0
294
257
227
185
159
135
125
112
100
084
2,5
273
240
213
173
150
127
117
105
095
079
3,0
253
222
197
164
142
121
111
100
092
075
3,5
232
206
185
155
133
115
106
095
087
072
4,0
213
190
172
145
125
110
100
090
083
070
4,5
195
177
160
135
117
105
094
086
080
067
5,0
178
162
148
127
110
098
089
082
076
064
5,5
163
150
137
120
105
094
084
077
072
062
6,0
150
138
128
112
098
090
080
073
068
060
6,5
136
127
118
103
094
085
076
070
065
058
7,0
125
117
108
096
090
081
072
067
062
056
8,0
105
100
092
086
082
072
065
060
056
052
9,0
090
087
081
077
072
065
058
055
050
048
10,0
080
076
071
068
064
057
052
048
044
044
Примечания
1 Значения коэффициентов φe в таблице увеличены в 1000 раз.
2 Значения φe  следует принимать не более значений φ.
Таблица Е.3 - Коэффициенты влияния формы сечения η
600 × 829 пикс.     Открыть в новом окне
349 × 833 пикс.     Открыть в новом окне
Таблица Е.4 - Приведенные относительные эксцентриситеты mef для внецентренно сжатых стержней с шарнирно-опертыми концами
Эпюры моментов
Значение mef при mef,1 , равном
0,1
0,5
1,0
1,5
2,0
3,0
4,0
5,0
7,0
10,0
20,0
1
0,10
0,30
0,68
1,12
1,60
2,62
3,55
4,55
6,50
9,40
19,40
2
0,10
0,17
0,39
0,68
1,03
1,80
2,75
3,72
5,65
8,60
18,50
3
0,10
0,10
0,22
0,36
0,55
1,17
1,95
2,77
4,60
7,40
17,20
4
0,10
0,10
0,10
0,18
0,30
0,57
1,03
1,78
3,35
5,90
15,40
5
0,10
0,10
0,10
0,10
0,15
0,23
0,48
0,95
2,18
4,40
13,40
6
0,10
0,10
0,10
0,10
0,10
0,15
0,18
0,40
1,25
3,00
11,40
7
0,10
0,10
0,10
0,10
0,10
0,10
0,10
0,10
0,50
1,70
9,50
1
0,10
0,31
0,68
1,12
1,60
2,62
3,55
4,55
6,50
9,40
19,40
2
0,10
0,22
0,46
0,73
1,05
1,88
2,75
3,72
5,65
8,60
18,50
3
0,10
0,17
0,38
0,58
0,80
1,33
2,00
2,77
4,60
7,40
17,20
4
0,10
0,14
0,32
0,49
0,66
1,05
1,52
2,22
3,50
5,90
15,40
5
0,10
0,10
0,26
0,41
0,57
0,95
1,38
1,80
2,95
4,70
13,40
6
0,10
0,16
0,28
0,40
0,52
0,95
1,25
1,60
2,50
4,00
11,50
7
0,10
0,22
0,32
0,42
0,55
0,95
1,10
1,35
2,20
3,50
10,80
1
0,10
0,32
0,70
1,12
1,60
2,62
2,55
4,55
6,50
9,40
19,40
2
0,10
0,28
0,60
0,90
1,28
1,96
2,75
3,72
5,65
8,40
18,50
3
0,10
0,27
0,55
0,84
1,15
1,75
2,43
3,17
4,80
7,40
17,20
4
0,10
0,26
0,52
0,78
1,10
1,60
2,20
2,83
4,00
6,30
15,40
5
0,10
0,25
0,52
0,78
1,10
1,55
2,10
2,78
3,85
5,90
14,50
6
0,10
0,28
0,52
0,78
1,10
1,55
2,00
2,70
3,80
5,60
13,80
7
0,10
0,32
0,52
0,78
1,10
1,55
1,90
2,60
3,75
5,50
13,00
1
0,10
0,40
0,80
1,23
1,68
2,62
3,55
4,55
6,50
9,10
19,40
2
0,10
0,40
0,78
1,20
1,60
2,30
3,15
4,10
5,85
8,60
18,50
3
0,10
0,40
0,77
1,17
1,55
2,30
3,10
3,90
5,55
8,13
18,00
4
0,10
0,40
0,75
1,13
1,55
2,30
3,05
3,80
5,30
7,60
17,50
5
0,10
0,40
0,75
1,10
1,55
2,30
3,00
3,80
5,30
7,60
17,00
6
0,10
0,40
0,75
1,10
1,50
2,30
3,00
3,80
5,30
7,60
16,50
7
0,10
0,40
0,75
1,10
1,40
2,30
3,00
3,80
5,30
7,60
16,00
Обозначения, принятые в таблице Е.4:
248 × 57 пикс.     Открыть в новом окне

Приложение Ж Виды креплений ограждающих конструкций

Таблица Ж.1
Описание крепления
Назначение продукции
Нормативные документы
Вытяжная алюминиевая заклепка с сердечником из нержавеющей стали или коррозионно-стойкие заклепки различного диаметра
Для крепления элементов примыкания и элементов конструкций между собой
ГОСТ 10299; ГОСТ 10300; ГОСТ 10301; ГОСТ 10304
Болтовое соединение
(в том числе шайба, гайка)
Для крепления элементов к несущей конструкции, а также элементов конструкций между собой
ГОСТ 7798; ГОСТ 5915
Винтовое соединение
Для крепления элементов конструкций между собой
ГОСТ 11738 ГОСТ 10618
Болты самоанкерующиеся распорные для строительства
Для крепления к стене
ГОСТ 28778

Приложение И Конструирование сварных соединений