ГОСТ Р 51910-2002 Методика исследования и проверки ускоренными методами влияния внешних воздействующих факторов на долговечность и сохраняемость технических изделий. Разработка и построение Читать онлайн бесплатно стр. 7

При ускорении режима испытаний по влажности при определении продолжительности испытаний согласно таблице A.1 вместо значения

подставляют значение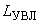

. Последнее определяют в соответствии с ГОСТ Р 51369.

Таблица А.2

Превышение испытательной температуры в ускоренном режиме над температурой по таблице A.1 , °С	Коэффициент ускорения испытаний для классов нагревостойкости электрической изоляции по ГОСТ 10518
	Y	А	Е	В	F	Н	200	220	250
10	2	2	2	1,5	2	2	2	1,5	2
20	4	4	3	3	4	4	4	3	4
30	7	7	5	5	6	7	6	5	6
40	13	10	10	10	10	13	10	10	15
50	22	20	15	12	17	22	17	17	22
60	35	30	20	22	30	35	35	40	30
70	65	45	35	35	50	60	55	65	40
80	100	70	55	50	70	10	90	100	70

А.3.6 Установленные в А.3.1- А.3.5 испытания, проводимые для подтверждения требований по показателям надежности, могут быть продолжены для определения фактических значений показателей. В этом случае испытания продолжают в тех же режимах до отказа всех контакторов, тем самым определяя срок службы

каждого контактора (образца).

Обработка результатов испытаний - в соответствии с приложением Б.

ПРИЛОЖЕНИЕ Б (рекомендуемое). Методика обработки результатов испытаний на гамма-процентный срок службы

Б.1 Результаты испытаний начинают обрабатывать с вычисления срока

, полученного при испытаниях каждого образца, где срок

- срок службы.

Срок

образцов, отказ которых определяют путем измерения параметров через определенные периоды испытаний, вычисляют как суммарное время за вычетом половины длительности последнего периода между испытаниями. Половину длительности не вычисляют, если методика определения параметров образца позволяет определить момент наступления отказа в процессе воздействия испытательных факторов.

Б.2 Определяют вид статистического распределения экспериментальных данных (логарифмически-нормальное распределение, распределение Вейбулла или нормальное распределение) по статистическим справочникам.

Если данные могут быть описаны двумя или тремя видами распределений или вид распределения не установлен, дальнейшую обработку проводят как для логарифмически-нормального распределения.

В Б.2-Б.7 приведен порядок вычисления необходимых параметров для статистических распределений логарифмически-нормального и Вейбулла. Порядок вычисления для нормального распределения приведен в Б.8.

Б.3 После определения вида статистического распределения экспериментальных данных вычисляют логарифмы каждого срока

и среднелогарифмический срок

(среднеарифметическое логарифмов сроков

)

, (Б.1)

где

- число испытуемых образцов;

Б.4 При необходимости результаты испытаний корректируют, исключая из рассмотрения образцы с резко выделяющимися значениями логарифмов сроков

согласно приложению 5 ГОСТ 10518.

Вычисляют среднелогарифмический корректированный срок

(среднеарифметическое логарифмов сроков

всех оставшихся для рассмотрения образцов)

Б.5 Определяют дисперсию

логарифмов сроков

по формуле

, (Б.2)

где

- число образцов, оставленных для рассмотрения.

Если в случае измерения критериев отказа в конце заданного интервала времени между измерениями все отказы произошли только в одном или двух интервалах времени между измерениями, то дисперсию

вычисляют по формуле

, (Б.3)

где

- логарифм длительности заданного интервала времени между измерениями;

- то же, что и в формуле (Б.1);

- большее число отказов, обнаруженное после одного или двух интервалов времени между измерениями (если после каждого из двух указанных интервалов времени обнаружено одинаковое число отказов,

= 0,5

; если все отказы обнаружены после одного интервала времени между измерениями,

);

- квантиль удвоенной нормированной функции Лапласа, определяемый по таблице Б.1 для требуемой вероятности

Б.6 Определяют

- среднее значение (математическое ожидание) логарифма гамма-процентного срока

(

выборки) по формуле

, (Б.4)

где

- квантиль нормированного нормального распределения по таблице Б.1 для требуемой вероятности

(для требуемого значения

);

Таблица Б.1

Доверительная вероятность или вероятность безотказной работы или хранения	Квантили нормального распределения

0,50	0	0,674
0,51	0,025	0,690
0,52	0,050	0,706
0,53	0,075	0,722
0,54	0,100	0,739
0,55	0,126	0,755
0,56	0,151	0,772
0,57	0,176	0,789
0,58	0,202	0,806
0,59	0,228	0,824
0,60	0,253	0,842
0,61	0,279	0,860
0,62	0,305	0,878
0,63	0,332	0,896
0,64	0,358	0,915
0,65	0,385	0,935
0,66	0,412	0,954
0,67	0,440	0,974
0,68	0,468	0,994
0,69	0,496	1,015
0,70	0,524	1,036
0,71	0,553	1,058
0,72	0,583	1,080
0,73	0,613	1,103
0,74	0,643	1,126
0,75	0,674	1,150
0,76	0,706	1,175
0,77	0,739	1,200
0,78	0,772	1,227
0,79	0,806	1,254
0,80	0,842	1,282
0,81	0,878	1,311
0,82	0,915	1,341
0,83	0,954	1,372
0,84	0,994	1,405
0,85	1,036	1,440
0,86	1,080	1,476
0,87	1,126	1,514
0,88	1,75	1,555
0,89	1,227	1,598
0,90	1,282	1,645
0,91	1,341	1,695
0,92	1,405	1,751
0,925	1,440	1,780
0,93	1,476	1,812
0,94	1,555	1,881
0,95	1,645	1,960
0,96	1,751	2,054
0,97	1,881	2,170
0,975	1,960	2,241
0,900	2,054	2,326
0,990	2,326	2,576
0,991	2,366	2,612
0,992	2,400	2,652
0,993	2,475	2,697
0,994	2,512	2,748
0,995	1,570	2,807
0,996	2,652	2,878
0,997	2,748	2,968
0,9975	2,807	3,024
0,9980	2,878	3,090
0,9990	3,090	3,291
0,9995	3,291	3,480
0,9999	3,719	3,885

Б.7 Определяют нижние доверительные границы для сроков

Б.7.1 Определяют нижнюю доверительную среднелогарифмическую границу значений сроков

при заданной доверительной вероятности

(или уровне значимости

) по формуле

, (Б.5)

где

- нижняя доверительная граница среднелогарифмического срока

при заданной доверительной вероятности

;

- распределение доверительных отклонений в малой выборке (распределение Стьюдента), определяемое по статистическим таблицам для заданного уровня доверительной вероятности

и числа степеней свободы