 |
|
| 1198 × 698 пикс.   Открыть в новом окне | |
_______________
* Дополнительный для расширения возможностей измерений
Рисунок 1 - Функциональная схема прибора
 |
|
| 450 × 306 пикс.   Открыть в новом окне | |
Рисунок 2а - Уровень фликера как функция времени
В качестве примера показано наличие сигнала в классе 7
 |
|
| 400 × 279 пикс.   Открыть в новом окне | |
Рисунок 2б - Интегральная функция вероятности наличия сигнала в классах 1-10
Рисунок 2 - Основные положения метода статистического анализа "время - уровень фликера"
ПРИЛОЖЕНИЕ А
(обязательное)
Способы повышения точности оценки фликера
Существуют различные способы обеспечения точности оценки фликера применительно к широкому диапазону условий. Некоторые из этих способов указаны ниже. При условии обеспечения установленной в настоящем стандарте погрешности измерений (±5%) для требуемого диапазона значений относительных изменений входного напряжения может быть применен любой из этих способов или их комбинация.
Во многих случаях частные значения уровней фликера 
, необходимые для вычисления 
, не будут соответствовать определенному классу и должны быть получены путем интерполяции (или экстраполяции) между имеющимися значениями.
, необходимые для вычисления , не будут соответствовать определенному классу и должны быть получены путем интерполяции (или экстраполяции) между имеющимися значениями.А.1 Линейная интерполяция
При линейной интерполяции полную шкалу классификатора 
разделяют на 
равных частей, так что интервал значений, соответствующий отдельному классу, составляет 
. Обозначим через 
номер класса, которому соответствует уровень фликера . Уровень фликера, соответствующий классу , расположен между значением 
, превышаемым в течение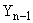 
процентов времени интервала наблюдений, и значением 
, превышаемым в течение 
процентов времени. При линейной интерполяции уровень фликера , соответствующий проценту времени 
, равен:
разделяют на равных частей, так что интервал значений, соответствующий отдельному классу, составляет . Обозначим через номер класса, которому соответствует уровень фликера . Уровень фликера, соответствующий классу , расположен между значением , превышаемым в течение процентов времени интервала наблюдений, и значением , превышаемым в течение процентов времени. При линейной интерполяции уровень фликера , соответствующий проценту времени , равен:
.A.2 Нелинейная интерполяция
Если линейная интерполяция не обеспечивает необходимой точности, используют нелинейную интерполяцию. При этом рекомендуется применять квадратичную формулу для уровней фликера, соответствующих трем смежным классам на интегральной функции вероятности. Значение определяют из выражения
определяют из выражения |
|
| 227 × 47 пикс.   Открыть в новом окне | |
где 
;
;
;
; - процент вероятности, соответствующий классу (см. А.1).А.3 Псевдонулевая точка пересечения
Может случиться, что одно или несколько значений уровней фликера , представляющих интерес, находится в интервале, принадлежащем первому классу.
, представляющих интерес, находится в интервале, принадлежащем первому классу.Опыт показывает, что интерполяция между нулевым значением и верхней границей первого класса приводит к ошибочным результатам, при этом подразумевается, что нулевой уровень будет превышен с вероятностью 100%. На практике кривая типовой интегральной функции вероятности может пересекать ось вероятностей в точке значительно ниже отметки 100% и затем проходить вертикально вверх по оси. Способ уменьшения ошибок в этой области заключается в экстраполяции кривой интегральной функции вероятности до пересечения с осью 
для получения псевдонулевой точки пересечения 
. определяют из следующего выражения:
для получения псевдонулевой точки пересечения . определяют из следующего выражения:
.А.4 Нелинейная шкала
Статистический анализ может быть более эффективным и точным, если классы имеют изменяемую ширину интервалов.
Может быть использована логарифмическая шкала, которая обычно позволяет применить линейную интерполяцию и избежать определения псевдонулевых точек пересечения. При этом обработка полного диапазона входных напряжений может осуществляться без переключения пределов измерений. С другой стороны, линейный классификатор может быть использован на выходе блока 3 прибора, но при этом необходимо переключение пределов измерений.
________________________________________________