Kz = KzoRz,
Kφ = Кφ0 Rφ,
Кх= Кх0 Rх.
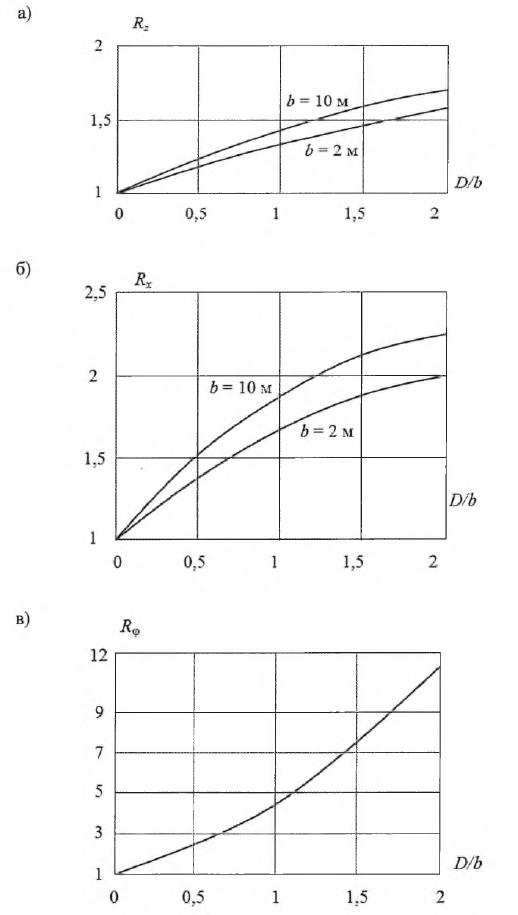
Коэффициенты Rz, Rφ, Rx определяются по рисунку 6.1 в зависимости от b и отношения D/b. Значение b принимается равным меньшей стороне подошвы фундамента — в случае вертикальных колебаний или стороне, параллельной направлению колебаний, — в случае горизонтально-вращательных колебаний.
Значения коэффициентов относительного демпфирования, учитывающие заглубление фундамента, определяются по формулам:
 | |
| 387 × 293 пикс. Открыть в новом окне | |
где
 | |
| 219 × 222 пикс. Открыть в новом окне | |
здесь Е — модуль деформации грунта;
- плотность грунта;
L — большая сторона подошвы фундамента при вертикальных колебаниях или сторона подошвы фундамента, перпендикулярная плоскости колебаний, при горизонтально-вращательных колебаниях;
т, ϴφ0 — то же, что в 6.2.5.
Значение ϴφ0,d вычисляется по формуле (50) с заменой ϴφ0 и h2 на ϴφ0,d и h2,d соответственно; значение к принимается равным 1,0 для песчаных грунтов; 1,2 — для супесей и суглинков; 1,8 — для глин.
 | |
| 518 × 915 пикс. Открыть в новом окне | |
а) — Rz; б) — Rx; в) — Rφ
Рисунок 6.1 — Графики определения коэффициентов Rz, Rφ, Rx для расчета коэффицентов жесткости оснований заглубленных фундаментов»
Сноску 2 к заголовку группы пунктов 6.2.1-6.2.4 «Рамные фундаменты2» изложить в новой редакции:
«2 Указания 6.2.1-6.2.4 относятся к машинам с периодическими нагрузками, имеющим частоту вращения не более 1000 об/мин. Для рамных фундаментов машин с частотой вращения более 1000 об/мин следует выполнять динамический расчет с учетом нескольких степеней свободы.».
Пункт 6.6.3. Изложить абзац «Ао, Во, Со - коэффициенты, зависящие от приведенной глубины погружения сваи  и условий опирания ее нижнего конца (определяются по указаниям СП 24.13330).» в новой редакции:
и условий опирания ее нижнего конца (определяются по указаниям СП 24.13330).» в новой редакции:
«Ао, Во, Со - коэффициенты, зависящие от приведенной глубины погружения сваи и условий опирания ее нижнего конца, определяемые по таблице 8а.».
Пункт 6.6.3. Дополнить таблицей 8а:
аблица 8а
Приведенная глубина погруже ния сваи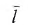
Приложение А (обязательное) Термины и определения
Дополнить терминами А.6 и А.7:
«А.6 экспонента матрицы (matrix exponential): Матричная функция от квадратной матрицы, аналогичная обычной экспоненциальной функции.
А.7 спектральная плотность мощности случайного процесса (stochastic process power spectral density): Функция, описывающая распределение мощности случайного процесса в зависимости от частоты.».
Приложение Б (рекомендуемое) Расчет колебаний несимметричных массивных и стенчатых фундаментов при произвольной зависимости нагрузки от времени
Дополнить пунктами Б.8-Б.13:
«Б.8 Для расчетов колебаний несимметричных массивных и стенчатых фундаментов рекомендуется использовать матричную форму:
| | |
| 284 × 44 пикс. Открыть в новом окне | |
где
— вектор-столбцы обобщенных координат и связанных с ними обобщенных сил; М', В' и К '— матрицы инерции, демпфирования и жесткости:
| | |
| 442 × 30 пикс. Открыть в новом окне | |
 | |
| 482 × 194 пикс. Открыть в новом окне | |
где т — масса фундамента с машиной;
— моменты инерции относительно осей выбранной прямоугольной системы координат и соответствующие центробежные моменты инерции; d'x, d'y, d'z — координаты центра масс;
| | |
| 236 × 27 пикс. Открыть в новом окне | |
| | |
| 218 × 32 пикс. Открыть в новом окне | |
| | |
| 222 × 43 пикс. Открыть в новом окне | |
Б.9 При задании вектора
действующих на фундамент обобщенных сил в системе координат Oxyz, не связанной с главными осями подошвы несимметричного фундамента, вектор f'(t) определяется по f(t):
| | |
| 235 × 29 пикс. Открыть в новом окне | |
 | |
| 540 × 183 пикс. Открыть в новом окне | |
dx, dy и dz— координаты точки О ' в системе Oxyz; ξ— угол, на который следует повернуть ось Ох (или Оу) вокруг оси Oz в положительном направлении для достижения ее параллельности и сонаправленности с осью О'х' (соответственно О'у'); оси Oz и O'z' параллельны и направлены вертикально вверх. В качестве системы координат Oxyz целесообразно выбирать систему координат, связанную с осями машины
Вектор обобщенных координат  в системе координат Oxyz определяется по q'(t):
в системе координат Oxyz определяется по q'(t):
q = ST q' (Б.11)
Периодические нагрузки
Б. 10 При вынужденных колебаниях с угловой частотой ω вектор периодических нагрузок (обобщенных сил) задается формулой
а решение матричного уравнения (Б.5) имеет вид
Постоянный вектор U' размера 6х 1 определяется из условия
 | |
| 262 × 53 пикс. Открыть в новом окне | |
Импульсные нагрузки
