MS− изгибающий момент в сечении панели в пролете;
MSB − изгибающий момент в сечении панели на промежуточной опоре В;
FB− опорная реакция на промежуточной опоре;
QSB – поперечная сила на промежуточной опоре В;
kτ− см. формулу (10).
7.2.2.3 Максимальные внутренние силы, возникающие в сечениях двухпролетной панели от воздействия разности температур на обшивках панели, определяются по формулам:
 | |
| 279 × 65 пикс. Открыть в новом окне | |
| | |
| 275 × 38 пикс. Открыть в новом окне | |
где 
kτ − см. формулу (10).
7.2.2.4 Внутренние силы, возникающие в сечениях трехпролетной панели от воздействия внешней равномерно распределенной нагрузки, вычисляют по формулам:
| | |
| 267 × 40 пикс. Открыть в новом окне | |
| | |
| 322 × 49 пикс. Открыть в новом окне | |
| | |
| 366 × 45 пикс. Открыть в новом окне | |
где kτ − см. формулу (10).
7.2.2.5 Внутренние силы, возникающие в сечениях трехпролетной панели
от воздействия разности температур на обшивках панели, вычисляют по формулам:
 | |
| 268 × 65 пикс. Открыть в новом окне | |
| | |
| 270 × 49 пикс. Открыть в новом окне | |
где 
kτ − см. формулу (10).
7.3 Трехслойные панели с профилированными поверхностями обшивок
7.3.1 Однопролетные панели
7.3.1.1 При расчете однопролетных панелей жесткость профилированных листов обшивки существенно влияет на распределение усилий в сечениях панели. В общем случае применяются численные методы расчета, например, с помощью метода конечных элементов.
7.3.1.2 При расчете панелей с профилированными обшивками принимают следующие характеристики жесткости обшивок и панелей в целом:
- при профилированных обшивках различной формы с обеих сторон панелей жесткость на единицу ширины панели:
| | |
| 229 × 37 пикс. Открыть в новом окне | |
| | |
| 276 × 38 пикс. Открыть в новом окне | |
- при одной профилированной и одной гладкой или слабо
профилированной обшивках панелей
| | |
| 210 × 39 пикс. Открыть в новом окне | |
-коэффициент сдвиговой податливости слоев панели с профилированными обшивками
где G – модуль сдвига слоев панели.
7.3.1.3 Изгибающие моменты и поперечные силы от равномерно распределенной нагрузки для однопролетных панелей с жесткими обшивками вычисляют по формулам:
| | |
| 331 × 43 пикс. Открыть в новом окне | |
Где kp− см. формулу (24).
7.3.2 Неразрезные многопролетные панели с профилированными обшивками
7.3.2.1 Напряжения в сечениях панелей и прогибы сплошных многослойных панелей с толстыми обшивками можно определить аналитически для часто встречающихся простых случаев.
7.3.2.2 Эпюры внутренних сил от воздействия внешней равномерно распределенной нагрузки и разности температур на обшивках в двухпролетных панелях приведены на рисунке 7.
а б
 | |
| 568 × 291 пикс. Открыть в новом окне | |
а – усилия в панели от постоянной нагрузки; б – усилия в панели от разности температур на обшивках; 1, 2 – пролеты
Рисунок 7 – Эпюры M и Q в трехслойных панелях и их обшивках от равномерно распределенной нагрузки
7.3.2.3 Изгибающие моменты и поперечные силы в сечениях двухпролетной неразрезной панели, в пролетах и на опорах А (крайняя) и В (промежуточная) от равномерно распределенной нагрузки вычисляют по формулам:
 | |
| 447 × 63 пикс. Открыть в новом окне | |
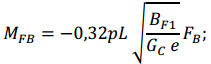 | |
| 211 × 64 пикс. Открыть в новом окне | |
 | |
| 439 × 70 пикс. Открыть в новом окне | |
