УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ постановлением Государственного комитета СССР по делам строительства от 2 декабря 1980 г. N 184
ВЗАМЕН ГОСТ 21778-76
ПЕРЕИЗДАНИЕ. Сентябрь 1988 г.
Настоящий стандарт распространяется на проектирование и строительство зданий и сооружений, а также на проектирование и изготовление строительных конструкций, деталей и изделий для них и устанавливает основные характеристики точности и основные положения по назначению, технологическому обеспечению, контролю и оценке точности геометрических параметров, обеспечивающие соблюдение функциональных требований к зданиям, сооружениям и их отдельным элементам на всех этапах строительного проектирования и производства.
Установленные настоящим стандартом основные положения развиваются комплексом стандартов Системы обеспечения точности геометрических параметров в строительстве.
В соответствии с требованиями стандартов Системы во вновь разрабатываемых и пересматриваемых стандартах и других нормативно-технических документах на конкретные элементы и конструкции зданий и сооружений, на рабочих чертежах и в технологической документации устанавливают требования к точности конструкций, их элементов и выполнения работ, а также методы и средства технологического обеспечения и контроля точности.
Применяемые в стандарте термины и их определения приведены в приложении 1.
Стандарт соответствует СТ СЭВ 2045-79 в части, указанной в приложении 2.
1. ХАРАКТЕРИСТИКИ ТОЧНОСТИ
1.1. Точность геометрического параметра 
, представляющего собой случайную величину, определяют характеристиками точности. При этом точность угловых величин может быть охарактеризована точностью линейных размеров, которыми определяются эти величины.
, представляющего собой случайную величину, определяют характеристиками точности. При этом точность угловых величин может быть охарактеризована точностью линейных размеров, которыми определяются эти величины. Характеристики точности геометрических параметров в строительстве и их взаимосвязь указаны на черт. 1.
Характеристики точности геометрического параметра
 | |
| 345 × 525 пикс. Открыть в новом окне | |
Черт. 1
1.2. Точность геометрического параметра 
в каждом отдельном случае характеризуется значением действительного отклонения 
, выражаемого зависимостью
в каждом отдельном случае характеризуется значением действительного отклонения , выражаемого зависимостью 
, (1)где 
- действительное значение параметра ;
- действительное значение параметра ; 
- номинальное значение параметра. Действительное отклонение является количественным выражением систематических и случайных погрешностей, накопленных при выполнении технологических операций и измерений.
является количественным выражением систематических и случайных погрешностей, накопленных при выполнении технологических операций и измерений. 1.3. Точность геометрических параметров в стандартах и других нормативных документах, а также на рабочих чертежах характеризуется минимальным 
и максимальным 
предельными размерами, нижним 
и верхним 
предельными отклонениями от номинального значения, допуском 
и отклонением 
середины поля допуска 
от номинального 
значения параметра 
. Половина допуска 
является предельным отклонением параметра х от середины поля допуска 
.
и максимальным предельными размерами, нижним и верхним предельными отклонениями от номинального значения, допуском и отклонением середины поля допуска от номинального значения параметра . Половина допуска является предельным отклонением параметра х от середины поля допуска . Взаимосвязь между этими характеристиками точности определяют по формулам:
, (2)
, (3)  | |
| 248 × 24 пикс. Открыть в новом окне | |
 | |
| 344 × 44 пикс. Открыть в новом окне | |
Примечание. Значения нижнего и верхнего предельных отклонений 
и 
подставляют в формулы со своими знаками.
и подставляют в формулы со своими знаками. 1.4. Точность геометрического параметра в совокупности его действительных значений 
, полученной в результате выполнения определенного технологического процесса или операции массового и серийного производства, определяют статистическими характеристиками точности.
в совокупности его действительных значений , полученной в результате выполнения определенного технологического процесса или операции массового и серийного производства, определяют статистическими характеристиками точности. В качестве статистических характеристик точности геометрического параметра применяют его среднее значение 
и среднее квадратическое отклонение 
. В необходимых случаях при различных законах распределения параметра допускается использовать другие статистические характеристики точности.
и среднее квадратическое отклонение . В необходимых случаях при различных законах распределения параметра допускается использовать другие статистические характеристики точности. При нормальном распределении геометрического параметра оценками характеристик и 
являются выборочное среднее 
и выборочное среднее квадратическое отклонение 
, которые вычисляют по формулам:
оценками характеристик и являются выборочное среднее и выборочное среднее квадратическое отклонение , которые вычисляют по формулам: 
, (6)
, (7)где 
-объем выборки.
-объем выборки. 1.5. Систематическое отклонение 
геометрического параметра определяют по формуле
геометрического параметра определяют по формуле 
. (8)Оценкой систематического отклонения 
, при нормальном распределении геометрического параметра является выборочное среднее отклонение 
, т. е. среднее значение отклонений в выборке, определяемое по формуле
, при нормальном распределении геометрического параметра является выборочное среднее отклонение , т. е. среднее значение отклонений в выборке, определяемое по формуле 
. (9)1.6. Предельные значения 
и устанавливают как значения геометрического параметра 
, отвечающие определенным вероятностям появления значений этого геометрического параметра ниже 
и выше . Взаимосвязь предельных значений 
и и статистических характеристик точности 
и представлена формулами:
и устанавливают как значения геометрического параметра , отвечающие определенным вероятностям появления значений этого геометрического параметра ниже и выше . Взаимосвязь предельных значений и и статистических характеристик точности и представлена формулами: 
, (10)
, (11)где 
и 
- значения стандартизованной случайной величины, зависящие от вероятности появления значений ниже 
и выше , и типа статистического распределения параметра .
и - значения стандартизованной случайной величины, зависящие от вероятности появления значений ниже и выше , и типа статистического распределения параметра . Как правило, вероятность появления значений ниже и выше принимают одинаковой, но не более 0,05.
ниже и выше принимают одинаковой, но не более 0,05. Предпочтительные значения величины 
при нормальном распределении параметра 
в зависимости от допускаемой вероятности появления значений 
ниже 
и выше 
, характеризуемой приемочным уровнем дефектности по ГОСТ 23616-79, установлены ГОСТ 23615-79.
при нормальном распределении параметра в зависимости от допускаемой вероятности появления значений ниже и выше , характеризуемой приемочным уровнем дефектности по ГОСТ 23616-79, установлены ГОСТ 23615-79. 1.7. В случае симметричного (например нормального) распределения геометрического параметра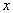 
(черт. 2) и одинаковой вероятности появления значений 
ниже и выше 
, а взаимосвязь между характеристиками точности, приведенными в пп. 1.3 и 1.4, представлена формулами:
(черт. 2) и одинаковой вероятности появления значений ниже и выше , а взаимосвязь между характеристиками точности, приведенными в пп. 1.3 и 1.4, представлена формулами: 
, (12)
, (13) 
. (14) Если при этом среднее значение 
параметра практически не отличается от его номинального значения 
, то взаимосвязь характеристик точности характеризуют формулы:
параметра практически не отличается от его номинального значения , то взаимосвязь характеристик точности характеризуют формулы: 
, (15) 
, (16)