Свод правил по проектированию и строительствуСП 52-101-2003"Бетонные и железобетонные конструкции без предварительного напряжения арматуры"(одобрен постановлением Госстроя РФ от 25 декабря 2003 г. N 215) стр. 10

; (6.46)

6.2.25 Расчет нормальных сечений железобетонных элементов по прочности производят из условий

; (6.47)

, (6.48)

где - относительная деформация наиболее сжатого волокна бетона в нормальном сечении элемента от действия внешней нагрузки;

- относительная деформация наиболее растянутого стержня арматуры в нормальном сечении элемента от действия внешней нагрузки;

- предельное значение относительной деформации бетона при сжатии, принимаемое согласно указаниям 6.2.31;

- предельное значение относительной деформации удлинения арматуры, принимаемое согласно указаниям 6.2.31.

6.2.26 Для железобетонных элементов, на которые действуют изгибающие моменты двух направлений и продольная сила (рисунок 6.7), деформации бетона и арматуры в нормальном сечении произвольной формы определяют из решения системы уравнений (6.49) - (6.51) с использованием уравнений (6.39) и (6.40):

; (6.49)

; (6.50)

. (6.51)

Жесткостные характеристики в уравнениях (6.49) - (6.51) определяют по формулам:

256 × 57 пикс.     Открыть в новом окне

; (6.52)

256 × 57 пикс.     Открыть в новом окне

; (6.53)

283 × 50 пикс.     Открыть в новом окне

; (6.54)

243 × 50 пикс.     Открыть в новом окне

; (6.55)

243 × 50 пикс.     Открыть в новом окне

; (6.56)

203 × 50 пикс.     Открыть в новом окне

. (6.57)

Обозначения в формулах см. 6.2.24.

6.2.27 Для железобетонных элементов, на которые действуют только изгибающие моменты двух направлений и (косой изгиб), в уравнении (6.51) принимают N = 0.

6.2.28 Для внецентренно сжатых в плоскости симметрии поперечного сечения железобетонных элементов и расположения оси X в этой плоскости и . В этом случае уравнения равновесия имеют вид:

; (6.58)

. (6.59)

6.2.29 Для изгибаемых в плоскости симметрии поперечного сечения железобетонных элементов и расположения оси X в этой плоскости N = 0, , . В этом случае уравнения равновесия имеют вид:

; (6.60)

; (6.61)

6.2.30 Расчет по прочности нормальных сечений внецентренно сжатых бетонных элементов, указанных в 4.1.2а, производят из условия (6.47) согласно указаниям 6.2.25 - 6.2.29, принимая в формулах 6.2.26 для определения 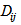площадь арматуры .

Для изгибаемых и внецентренно сжатых бетонных элементов, в которых не допускаются трещины, расчет производят с учетом работы растянутого бетона в поперечном сечении элемента из условия

, (6.62)

где - относительная деформация наиболее растянутого волокна бетона в нормальном сечении элемента от действия внешней нагрузки, определяемая согласно 6.2.26 - 6.2.29;

- предельное значение относительной деформации бетона при растяжении, принимаемое согласно указаниям 6.2.31.

6.2.31 Предельные значения относительных деформаций бетона принимают при двузначной эпюре деформаций (сжатие и растяжение) в поперечном сечении бетона элемента (изгиб, внецентренное сжатие или растяжение с большими эксцентриситетами) равными .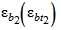

При внецентренном сжатии или растяжении элементов и распределении в поперечном сечении бетона элемента деформаций только одного знака предельные значения относительных деформаций бетона определяют в зависимости от соотношения деформаций бетона на противоположных гранях сечения элемента и по формулам:

; (6.63)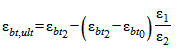

; (6.64)

где , , , - деформационные параметры расчетных диаграмм состояния бетона (5.1.12, 5.1.18, 5.1.20).

Предельное значение относительной деформации арматуры принимают равным 0,025.

Расчет по прочности железобетонных элементов при действии поперечных сил

Общие положения

6.2.32 Расчет по прочности железобетонных элементов при действии поперечных сил производят на основе модели наклонных сечений.

При расчете по модели наклонных сечений должны быть обеспечены прочность элемента по полосе между наклонными сечениями и по наклонному сечению на действие поперечных сил, а также прочность по наклонному сечению на действие момента.

Прочность по наклонной полосе характеризуется максимальным значением поперечной силы, которое может быть воспринято наклонной полосой, находящейся под воздействием сжимающих усилий вдоль полосы и растягивающих усилий от поперечной арматуры, пересекающей наклонную полосу. При этом прочность бетона определяют по сопротивлению бетона осевому сжатию с учетом влияния сложного напряженного состояния в наклонной полосе.

Расчет по наклонному сечению на действие поперечных сил производят на основе уравнения равновесия внешних и внутренних поперечных сил, действующих в наклонном сечении с длиной проекции с на продольную ось элемента. Внутренние поперечные силы включают поперечную силу, воспринимаемую бетоном в наклонном сечении, и поперечную силу, воспринимаемую пересекающей наклонное сечение поперечной арматурой. При этом поперечные силы, воспринимаемые бетоном и поперечной арматурой, определяют по сопротивлениям бетона и поперечной арматуры растяжению с учетом длины проекции с наклонного сечения.

Расчет по наклонному сечению на действие момента производят на основе уравнения равновесия моментов от внешних и внутренних сил, действующих в наклонном сечении с длиной проекции с на продольную ось элемента. Моменты от внутренних сил включают момент, воспринимаемый пересекающей наклонное сечение продольной растянутой арматурой, и момент, воспринимаемый пересекающей наклонное сечение поперечной арматурой. При этом моменты, воспринимаемые продольной и поперечной арматурой, определяют по сопротивлениям продольной и поперечной арматуры растяжению с учетом длины проекции с наклонного сечения.

Расчет железобетонных элементов по полосе между наклонными сечениями

6.2.33 Расчет изгибаемых железобетонных элементов по бетонной полосе между наклонными сечениями производят из условия

, (6.65)

где Q - поперечная сила в нормальном сечении элемента;

- коэффициент, принимаемый равным 0,3.