Усилия  и
и 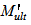 определяют по формулам:
определяют по формулам:
б) если продольная сила N приложена за пределами расстояния между равнодействующими усилий в арматуре S и S' (рисунок 6.6, б), из условия (6.30) определяют предельный момент  по формуле
по формуле
| | |
| 241 × 27 пикс. Открыть в новом окне | |
 | |
| 2000 × 2124 пикс. Открыть в новом окне | |
при этом высоту сжатой зоны х определяют по формуле
 . (6.35)
. (6.35) Если полученное из расчета по формуле (6.35) значение  , в формулу (6.34) подставляют
, в формулу (6.34) подставляют 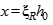 , где
, где  определяют согласно указаниям 6.2.7.
определяют согласно указаниям 6.2.7.
Расчет по прочности нормальных сечений на основе нелинейной деформационной модели
6.2.21 При расчете по прочности усилия и деформации в сечении, нормальном к продольной оси элемента, определяют на основе нелинейной деформационной модели, использующей уравнения равновесия внешних сил и внутренних усилий в сечении элемента, а также следующие положения:
- распределение относительных деформаций бетона и арматуры по высоте сечения элемента принимают по линейному закону (гипотеза плоских сечений);
- связь между осевыми напряжениями и относительными деформациями бетона и арматуры принимают в виде диаграмм состояния (деформирования) бетона и арматуры (5.1.17, 5.2.11);
- сопротивление бетона растянутой зоны допускается не учитывать, принимая при  напряжения
напряжения  . В отдельных случаях (например, изгибаемые и внецентренно сжатые бетонные конструкции, в которых не допускают трещины) расчет по прочности производят с учетом работы растянутого бетона.
. В отдельных случаях (например, изгибаемые и внецентренно сжатые бетонные конструкции, в которых не допускают трещины) расчет по прочности производят с учетом работы растянутого бетона.
6.2.22 Переход от эпюры напряжений в бетоне к обобщенным внутренним усилиям определяют с помощью процедуры численного интегрирования напряжений по нормальному сечению. Для этого нормальное сечение условно разделяют на малые участки: при косом внецентренном сжатии (растяжении) и косом изгибе - по высоте и ширине сечения; при внецентренном сжатии (растяжении) и изгибе в плоскости оси симметрии поперечного сечения элемента - только по высоте сечения. Напряжения в пределах малых участков принимают равномерно распределенными (усредненными).
6.2.23 При расчете элементов с использованием деформационной модели принимают:
- значения сжимающей продольной силы, а также сжимающих напряжений и деформаций укорочения бетона и арматуры - со знаком "минус";
- значения растягивающей продольной силы, а также растягивающих напряжений и деформаций удлинения бетона и арматуры - со знаком "плюс".
Знаки координат центров тяжести арматурных стержней и выделенных участков бетона, а также точки приложения продольной силы принимают в соответствии с назначенной системой координат XOY. В общем случае начало координат этой системы (точка О на рисунке 6.7) располагают в произвольном месте в пределах поперечного сечения элемента.
 | |
| 1075 × 1365 пикс. Открыть в новом окне | |
6.2.24 При расчете нормальных сечений по прочности (рисунок 6.7) в общем случае используют:
уравнения равновесия внешних сил и внутренних усилий в нормальном сечении элемента:
 | |
| 215 × 50 пикс. Открыть в новом окне | |
 | |
| 217 × 50 пикс. Открыть в новом окне | |
 ; (6.38)
; (6.38) уравнения, определяющие распределение деформаций по сечению элемента:
зависимости, связывающие напряжения и относительные деформации бетона и арматуры:
В уравнениях (6.36) - (6.42):
где  ,
, 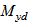 - изгибающие моменты в соответствующих плоскостях от внешней нагрузки, определяемые из статического расчета конструкции;
- изгибающие моменты в соответствующих плоскостях от внешней нагрузки, определяемые из статического расчета конструкции;
N - продольная сила от внешней нагрузки;
Коэффициенты  и
и  принимают по соответствующим диаграммам состояния бетона и арматуры, указанным в 5.1.17, 5.2.11.
принимают по соответствующим диаграммам состояния бетона и арматуры, указанным в 5.1.17, 5.2.11.
Значения коэффициентов  и
и  определяют как соотношение значений напряжений и деформаций для рассматриваемых точек соответствующих диаграмм состояния бетона и арматуры, принятых в расчете, деленное на модуль упругости бетона
определяют как соотношение значений напряжений и деформаций для рассматриваемых точек соответствующих диаграмм состояния бетона и арматуры, принятых в расчете, деленное на модуль упругости бетона  и арматуры
и арматуры  (при двухлинейной диаграмме состояния бетона - на приведенный модуль деформации
(при двухлинейной диаграмме состояния бетона - на приведенный модуль деформации  ). При этом используют зависимости "напряжение - деформация" (5.4) - (5.8), (5.12) и (5.13) на рассматриваемых участках диаграмм.
). При этом используют зависимости "напряжение - деформация" (5.4) - (5.8), (5.12) и (5.13) на рассматриваемых участках диаграмм.
 ; (6.45)
; (6.45)