при 
при 
при  напряжение
напряжение  следует определять линейной интерполяцией.
следует определять линейной интерполяцией.
Здесь - длина цилиндрической оболочки.
Та же оболочка, но укрепленная кольцевыми ребрами, расположенными с шагом  между осями, должна быть рассчитана на устойчивость по формулам (159)-(161) с подстановкой в них значения s вместо .
между осями, должна быть рассчитана на устойчивость по формулам (159)-(161) с подстановкой в них значения s вместо .
В этом случае должно быть удовлетворено условие устойчивости ребра в своей плоскости как сжатого стержня согласно требованиям 7.1.3 при N=prs и расчетной длине стержня 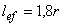 ; при этом в сечение ребра следует включать участки оболочки шириной
; при этом в сечение ребра следует включать участки оболочки шириной 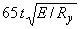 с каждой стороны от оси ребра, а условная гибкость стержня
с каждой стороны от оси ребра, а условная гибкость стержня  не должна превышать 6,5.
не должна превышать 6,5.
При одностороннем ребре жесткости его момент инерции следует вычислять относительно оси, совпадающей с ближайшей поверхностью оболочки.
11.2.5 Расчет на устойчивость замкнутой круговой цилиндрической оболочки вращения, подверженной одновременному действию нагрузок, указанных в 11.2.1 и 11.2.4, следует выполнять по формуле
где должно быть вычислено согласно требованиям 11.2.1 и - согласно требованиям 11.2.4.
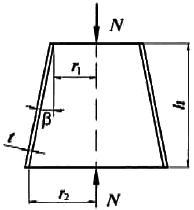
11.2.6 Расчет на устойчивость конической оболочки вращения с углом конусности  60°, сжатой силой N вдоль оси (рисунок 18), следует выполнять по формуле
60°, сжатой силой N вдоль оси (рисунок 18), следует выполнять по формуле
где  - критическая сила, определяемая по формуле
- критическая сила, определяемая по формуле
здесь t - толщина оболочки;
- значение напряжения, вычисленное согласно требованиям 11.2.1 с заменой радиуса  радиусом
радиусом  , равным
, равным
11.2.7 Расчет на устойчивость конической оболочки вращения при действии внешнего равномерного давления р, нормального к боковой поверхности, следует выполнять по формуле
, (166)
 | |
| 194 × 210 пикс. Открыть в новом окне | |
Рисунок 18 - Схема конической оболочки вращения под действием продольного усилия сжатия
здесь  - расчетное кольцевое напряжение в оболочке;
- расчетное кольцевое напряжение в оболочке;
- критическое напряжение, определяемое по формуле
где - радиус, определяемый по формуле (165);
h - высота конической оболочки (между основаниями).
11.2.8 Расчет на устойчивость конической оболочки вращения, подверженной одновременному действию нагрузок, указанных в 11.2.6 и 11.2.7, следует выполнять по формуле
где значения и следует вычислять по формулам (164) и (167).
11.2.9 Расчет на устойчивость полной сферической оболочки (или ее сегмента) при  750 и действии внешнего равномерного давления р, нормального к ее поверхности, следует выполнять по формуле
750 и действии внешнего равномерного давления р, нормального к ее поверхности, следует выполнять по формуле
где  - расчетное напряжение;
- расчетное напряжение;
здесь r - радиус срединной поверхности сферы.
12 Расчет элементов стальных конструкций на усталость
12.1 Общие положения расчета
12.1.1 При проектировании стальных конструкций и их элементов (балки крановых путей, балки рабочих площадок, элементы конструкций бункерных и разгрузочных эстакад, конструкции под двигатели и др.), непосредственно воспринимающих многократно действующие подвижные, вибрационные или другого вида нагрузки с количеством циклов нагружений 10 и более, приводящие к явлению усталости, следует применять такие конструктивные решения, которые не вызывают значительной концентрации напряжений, и проверять расчетом на усталость.
и более, приводящие к явлению усталости, следует применять такие конструктивные решения, которые не вызывают значительной концентрации напряжений, и проверять расчетом на усталость.
Количество циклов нагружений следует принимать по технологическим требованиям эксплуатации.
Расчет конструкций на усталость следует производить на действие нагрузок, устанавливаемых согласно СП 20.13330 .
Расчет на усталость также следует выполнять для конструкций высоких сооружений (типа мачт, башен и т.п.), которые подвергаются воздействиям резонансного вихревого возбуждения согласно СП 20.13330 .
12.1.2 Расчет на усталость следует производить по формуле
где  - наибольшее по абсолютному значению напряжение в рассчитываемом сечении элемента, вычисленное по сечению нетто без учета коэффициента динамичности и коэффициентов , ,
- наибольшее по абсолютному значению напряжение в рассчитываемом сечении элемента, вычисленное по сечению нетто без учета коэффициента динамичности и коэффициентов , , 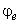 ;
;
при  3,9·10
3,9·10 , принимаемый равным =0,77;
, принимаемый равным =0,77;
