от начала внутреннего закругления до края полки – в прокатных профилях; от края выкружки до края полки – в гнутых профилях (см. рисунок 5).
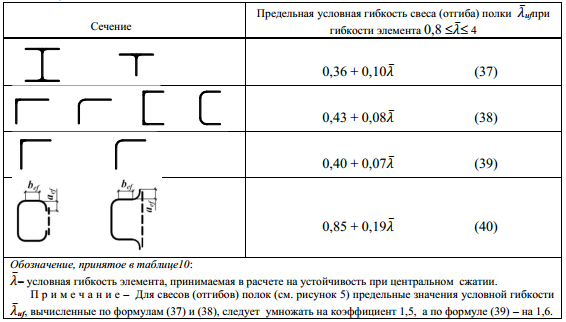
7.3.8 Устойчивость поясных листов и полок центрально сжатых элементов сплошного сечения следует считать обеспеченной, если условная гибкость свеса пояса (полки)
не превышает значений предельной условной гибкости свеса пояса (полки) 
определяемых по формулам таблицы 10, в которых при значениях 
следует принимать соответственно 
Т а б л и ц а 10
 | |
| 566 × 322 пикс. Открыть в новом окне | |
7.3.9 В центрально сжатых элементах коробчатого сечения предельную условную гибкость поясного листа ̅λuf,1 следует принимать по таблице 10, как для стенок коробчатого сечения: 
7.3.10 Высота отгиба полки (стенки) аef (см. рисунок 5) должна быть не менее 0,3 bef в элементах, не усиленных планками, и 0,2 bef – в элементах, усиленных планками (см. таблицу 10); при этом толщина ребра должна быть не менее 
7.3.11 При назначении сечений центральносжатых элементов по предельной гибкости (в соответствии с 10.4) значения предельных условных гибкостей стенки ̅λuw и поясов ̅λuf ( ̅λuf,1), определяемых по таблицам 9 и 10 соответственно, следует увеличивать умножением на коэффициент 
, но не более чем на 1,25.
, но не более чем на 1,25.8 Расчет элементов стальных конструкций при изгибе
8.1 Общие положения расчета
В зависимости от назначения и условий эксплуатации конструкцийрасчёт изгибаемых элементов (балок) следует выполнять без учёта или сучётом пластических деформаций в соответствии с подразделением элементов на три класса согласно 4.2.7.
Балки 1-го класса следует применять для нагрузок всех видов и рассчитывать в пределах упругих деформаций; балки 2-го и 3-го классов следует применять для статическихнагрузок и рассчитывать с учётом развития пластических деформаций.
Балки крановых путей под краны групп режимов работы 1К – 8К по ГОСТ 25546 при расчёте на прочность следует относить к 1-му классу.
Бистальные балки следует относить ко 2-му классу и рассчитывать с учётом ограниченных пластических деформаций в стенке, значения которых следует определять придостижении расчётного сопротивления Ryf в поясах, выполненных из более прочной стали.
8.2 Расчет на прочность изгибаемых элементов сплошного сечения
8.2.1 Расчёт на прочность балок 1-го класса следует выполнять по формулам:
при действии момента в одной из главных плоскостей
(41) при действии в сечении поперечной силы
(42)при действии моментов в двух главных плоскостях (и наличии бимомента)
 | |
| 265 × 39 пикс. Открыть в новом окне | |
где х и у - расстояния от главных осей до рассматриваемой точки сечения, а
ω–секториальная координата этой точки;
при одновременном действии в стенке балки момента и поперечной силы
 | |
| 308 × 37 пикс. Открыть в новом окне | |
где σх =Mxy/Ixn - нормальное напряжение в срединной плоскости стенки, параллельноепродольной оси балки;
σу - то же, перпендикулярное к продольной оси балки, в том числе σloc, определяемое по формуле (47);
τху = QS/(Itw) - касательное напряжение в стенке.
Напряжения σх и σу, принимаемые в формуле (44) со своими знаками, а также τху следует определять в одной и той же точке стенки балки.
При проверке прочности на действие поперечной силы на опоре для разрезных балок формулу (42) следует использовать без учета работы поясов.
В балках, рассчитываемых по формуле (43), значения напряжений в стенке балки должны быть проверены по формуле (44) в двух главных плоскостях изгиба.
При ослаблении стенки отверстиями для болтов левую часть формулы (42), a также значение τху в формуле (44), следуетумножатьна коэффициент α, определяемый поформуле
α= s/(s – d), (45)
где s – шаг отверстий в одном вертикальном ряду;
d– диаметр отверстия.
8.2.2 Расчёт на прочность стенки балки, не укрепленной ребрами жёсткости, при действии местного напряжения σloc в местах приложения нагрузки к верхнему поясу, а также в опорных сечениях балки, следует выполнять по формуле
(46) где σloc = F /(lef tw). (47)
Здесь F – расчётное значение нагрузки (силы);
lef– условная длина распределения нагрузки, определяемая по формулам:
для случаев по рисунку 6,а) и б)
lef= b + 2h; (48)
для случая по рисунку 6,в
(49)  | |
| 502 × 175 пикс. Открыть в новом окне | |
а) – сварная балка; б) – прокатная балка; в) – сварная или прокатная балки при нагрузкеот колеса крана
Рисунок 6 – Схемы распределения сосредоточенной нагрузки на стенку балки
где h – размер, равный сумме толщины верхнего пояса балки и катета поясного шва, если нижняя балка сварная (см. рисунок 6,а), либо расстоянию от наружной грани полки до начала внутреннего закругления стенки, если нижняябалка прокатная (см. рисунок 6,б);
Ψ– коэффициент, принимаемый равным: 3,25 – для сварных и прокатных балок;