5.13 (5.6). Формулы табл. 7 СНиП II-23-81* (тип сечения 3) для определения для трехгранных сквозных стержней основаны на рассмотрении их потери устойчивости в плоскостях х-х и у-у в предположении неизменности расстояний между ветвями стержня при изгибе.
5.14 (5.6). Формулы табл. 13 настоящего Пособия получены без учета влияния начальных несовершенств и продольных сил в ветвях на значение угла сдвига . В связи с этим в СНиП II-23-81* введены ограничения на значения гибкостей отдельных ветвей.
Для стержней с планками гибкость отдельной ветви, при которой влияние указанных факторов несущественно, составляет 40.
При большем значении формулы для и необходимо уточнять заменой выражений и соответственно на и , где (здесь - коэффициент, вычисляемый для стержня по приведенной гибкости ).
Таблица 13
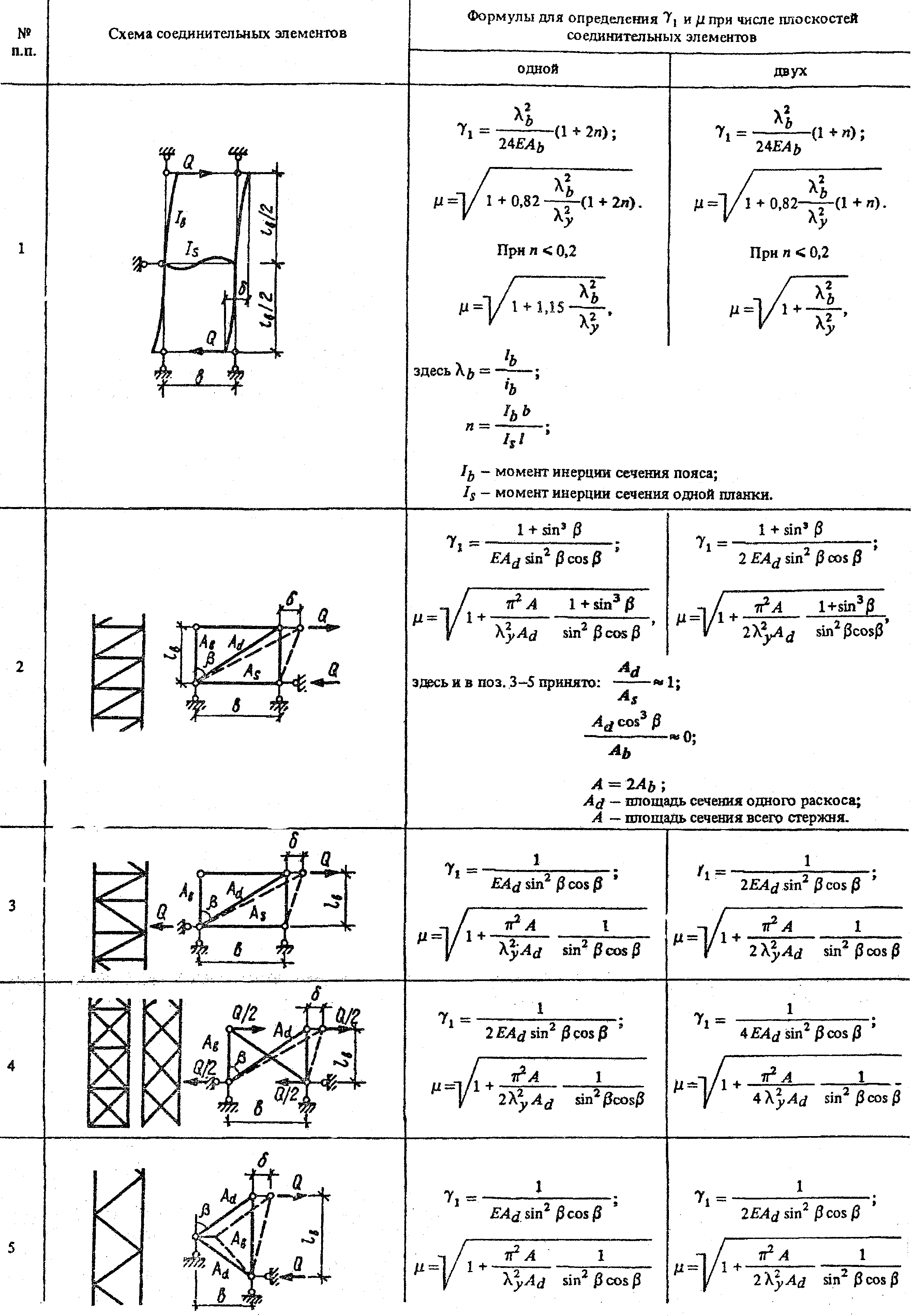 | |
| 2675 × 3862 пикс. Открыть в новом окне | |
5.15 (5.6). При расчете сквозных решетчатых стержней начальные несовершенства обычно учитываются коэффициентом в формуле (7) СНиП II-23-81* на стадии подбора сечения всего стержня и проверки устойчивости его отдельных ветвей. В то же время имеются работы*(3); *(4), в которых показано, что на несущую способность сквозного стержня с решетками существенное влияние оказывают увеличение гибкости панели, а также начальные искривления стержня и отдельных панелей. В связи с этим в п. 5.6 СНиП II-23-81* введены ограничения на значения гибкостей отдельных ветвей между узлами.
В ряде случаев при эти ограничения согласно СНиП II-23-81* могут быть сняты. При этом требуется выполнить расчет сквозного стержня по деформированной схеме, которую можно учесть приближенным практическим способом расчета, существо которого сводится к следующему:
если гибкость отдельной ветви на участке между узлами , то расчетное сопротивление при проверке сквозного стержня с решетками по формулам (7) или (51) СНиП II-23-81* может быть принято равным (правые части этих формул будут равны ), здесь - коэффициент продольного изгиба для отдельной ветви, расчетную гибкость которой можно принять ; коэффициенты и в формулах (7) и (51) СНиП II-23-81* необходимо принимать соответственно по табл. 72 и 75 СНиП II-23-81* при указанном расчетном сопротивлении в зависимости от и ;
при значение принимается равным 1,0, а в интервале - по линейной интерполяции между 1,0 и значением при .
Коэффициент расчетной длины при приближенно учитывает взаимодействие ветви колонны с элементами решетки, а также вероятность одновременного совпадения расчетных значений начальных несовершенств для всего стержня и отдельной панели ветви.
5.16 (5.7). Соединение составных стержней вплотную или через прокладки обеспечивает совместную работу составляющих его элементов и равномерное распределение между ними продольной силы.
Для сжатых стержней длина участка между соединениями равна 40i, что соответствует гибкости в сквозных стержнях с планками. При этом влияние продольной силы на деформирование элементов, составляющих стержень, несущественно (см. п. 5.14 настоящего Пособия).
5.17 (5.8*). Условная поперечная сила определяется как проекция продольной сжимающей силы N на ось, перпендикулярную изогнутой оси шарнирно опертого внецентренно-сжатого с эксцентриситетом стержня сквозного сечения, имеющего начальное искривление , в его предельном состоянии (рис. 5) и вычисляется по формуле
. (31)
 | |
| 1171 × 1234 пикс. Открыть в новом окне | |
Для синусоидальной формы начального искривления и изогнутой оси стержня получим
. (32)
Для вычисления и были определены предельные параметры внецентренно-сжатого стержня идеализированного сечения, состоящего из двух одинаковых полок, связанных между собой жесткой связью (см. рис. 5, б). Влияние решетки на предельное значение учитывалось введением приведенной гибкости по формуле (17) СНиП II-23-81*.
Полученные значения для различных и аппроксимированы в СНиП II-23-81* приближенной зависимостью
, (33)
которая учитывает возможность недонапряжения сквозного стержня в плоскости соединительных элементов; здесь .
Значения множителя k при в правой части формулы (33) для различных значений расчетных сопротивлений и МПа приведены в табл. 14.
Таблица 14
R_y, МПа (кгс/см2) | k | R_y, МПа (кгс/см2) | k |
210 (2150) | 0,0097 | 330 (3350) | 0,0122 |
230 (2350) | 0,0103 | 350 (3550) | 0,0125 |
250 (2550) | 0,0108 | 370 (3750) | 0,0127 |
270 (2750) | 0,0112 | 400 (4100) | 0,0130 |
300 (3050) | 0,0118 | 500 (5100) | 0,0137 |
5.18 (5.10). Для определения дополнительных усилий в раскосах перекрестной решетки с целью учета влияния обжатия поясов в сквозных стержнях рассматривается один раз статически неопределимая система, схема которой приведена на рис. 6, а. Разрез одного из раскосов дает основную систему, схемы нагружения которой показаны на рис. 6, б, в.
 | |
| 1300 × 879 пикс. Открыть в новом окне | |
Из решения рассматриваемой задачи получено дополнительное усилие, возникающее в раскосах
. (34)
где .
Принимая и , можно получить формулу (26) СНиП II-23-81*.
Принимая обозначения и , получим
, (35)
Значения отношения для различных приведены в табл. 15.
Таблица 15
дельта | 0,5 | 0,6 | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 |
0,082 | 0,117 | 0,200 | 0,293 | 0,396 | 0,475 | 0,554 | 0,620 |
Получаемое таким образом дополнительное усилие в раскосах от обжатия поясов стержня сжимающей силой необходимо прибавить к усилию в раскосах от условной (или фактической) поперечной силы Q.
5.19 (5.11). Расчет стержней, предназначенных для уменьшения расчетной длины сжатых элементов, необходимо выполнять на усилие, равное и определяемое с использованием данных табл. 14 и формулы (33) в зависимости от продольной силы N и коэффициента продольного изгиба для основного подкрепляемого элемента.
Расчет распорок, предназначенных для уменьшения расчетной длины колонн в направлении вдоль здания (из плоскости рам), при наличии нагрузок от мостовых кранов допускается выполнять на усилие, определяемое по формуле (33), в которой значение N принимается равным сумме продольных сил в двух соседних колоннах.
Изгибаемые элементы
5.20 (5.14*). В балках, рассчитываемых в пределах упругих деформаций, необходимо проверять прочность стенки при сложном напряженном состоянии путем определения обобщенного напряжения (интенсивности напряжений) на основе энергетической теории прочности по формуле (33) СНиП II-23-81*. Обобщенное напряжение, вычисляемое по этой формуле, сравнивается с расчетным сопротивлением, увеличенным на 15%, что предполагает развитие локальных неупругих деформаций в стенке.
Указанный расчет необходимо выполнять в первую очередь для проверки стенок двутавровых балок в месте соединения стенки с верхним поясом. При этом в стенках разрезных балок напряжения и обычно имеют одинаковые знаки, в то время как в сечениях у опор неразрезных балок эти напряжения могут иметь разные знаки, что необходимо учитывать при пользовании формулой (33) СНиП II-23-81*.
5.21 (5.15). Для определения критических напряжений при потере устойчивости балок двутаврового сечения с двумя осями симметрии, изгибаемых в плоскости стенки, были использованы результаты работ С.П. Тимошенко [13], которые для практических расчетов представлены в СНиП II-23-81* в виде формул (34) и (174). Необходимо подчеркнуть, что в работе [13] исследовались идеальные упругие балки. Для расчета реальных стальных балок в формуле (34) СНиП II-23-81* влияние начальных несовершенств (в частности, начального искривления оси балки в плоскости наименьшей жесткости) учтено при выводе формул для коэффициента , а также введением коэффициента условий работы (см. поз. 4 табл. 6* СНиП II-23-81*).
Коэффициенты в табл. 77 СНиП II-23-81* приведены для случая шарнирного опирания в плоскости наименьшей жесткости и свободной депланации концов расчетного участка балки.
Значения вычислены в предположении, что . Если отношение не очень мало, то значения следует умножать на .
Для балок двутаврового сечения с одной осью симметрии коэффициенты и , определяемые по формулам (177) и (178) СНиП II-23-81*, были получены в работе [14] на основе использования уравнений В.3. Власова при указанных граничных условиях.
5.22 (5.15). Для случая, когда критические напряжения при потере устойчивости балок превышают предел пропорциональности, методика расчета разработана на основе исследования соотношения между критическим напряжением неограниченно упругого центрально-сжатого стержня и действительным напряжением следующего вида:
. (36)
В формуле (36) предел пропорциональности принят равным , а отношение при , что эквивалентно отношению (где - приведенный модуль).
