Государственный стандарт Союза ССР ГОСТ 16493-70 "Качество продукции. Статистический приемочный контроль по альтернативному признаку. Случай недопустимости дефектных изделий в выборке" (утв. постановлением Госстандарта СССР от 15 января 1970 г. N 1758) стр. 10

_

б) доверительные границы для среднего уровня выходного качества q_в в процентах вычисляют

по формулам:

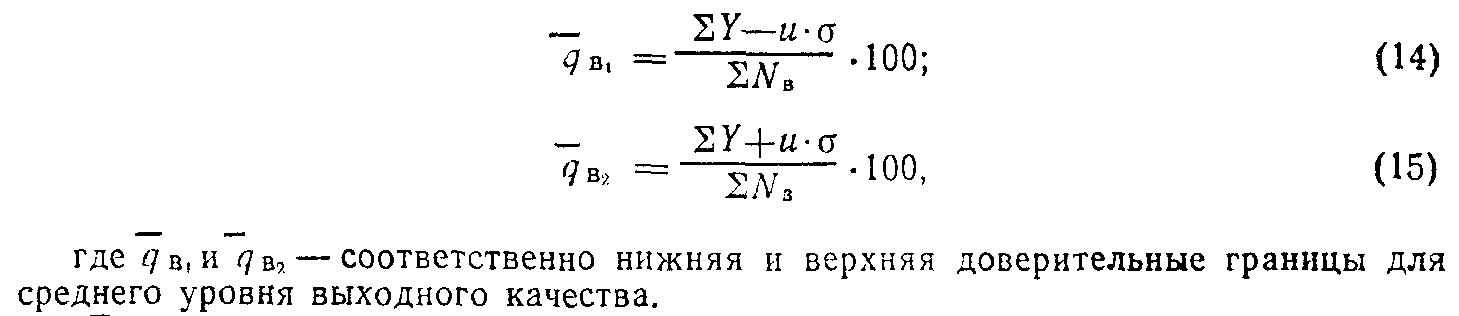1459 × 316 пикс.     Открыть в новом окне

Если в результате вычисления по формуле (14) получается отрицательное число, нижнюю доверительную границу для среднего уровня выходного качества следует считать равной нулю.

4.3. Доверительные границы для среднего уровня выходного качества для варианта браковки КЗ следует вычислять по методике, приведенной в п. 4.1, со следующими изменениями:

а) вместо вычисления суммы Сумма Х суммируют значения Сумма Y, приведенные в графе 12;

_

б) доверительные границы для среднего уровня выходного качества q_в в процентах вычисляют

по формулам:

1447 × 316 пикс.     Открыть в новом окне

Если в результате вычисления по формуле (16) получается отрицательное число, то нижнюю доверительную границу для среднего уровня выходного качества следует считать равной нулю.

Таблица 1

Значения коэффициента К_0

┌──────────┬────────────────────────────────────────────────────────────┐
│ Уровни │ Значения коэффициента К_0 при среднем относительном объеме │
│доверите- │ выборки │
│ льной │ _ │
│вероятнос-│ лямбда │
│ ти ню ├─────────┬─────────┬─────────┬──────────┬─────────┬─────────┤
│ │ 0,0 │ 0,1 │ 0,2 │ 0,3 │ 0,4 │ 0,5 │
├──────────┼─────────┼─────────┼─────────┼──────────┼─────────┼─────────┤
│ 0,90 │ 6,4 │ 3,8 │ 1,9 │ 1,5 │ 1,3 │ 1,2 │
│ │ │ │ │ │ │ │
│ 0,95 │ 9,0 │ 5,3 │ 2,5 │ 1,8 │ 1,5 │ 1,3 │
└──────────┴─────────┴─────────┴─────────┴──────────┴─────────┴─────────┘

Таблица 2

Значения коэффициента К_1

┌─────────┬───────────────────────────────────────────────┬─────────────────────────────────────────────────┐
│Суммарное│ Значения коэффициента К_1 при доверительной │ Значения коэффициента K_1 при доверительной │
│ число │ вероятности ню=0,90 и среднем относительном │ вероятности ню=0,95 и среднем относительном │
│дефектных│ объеме │ объеме │
│ изделий │ _ │ _ │
│ Сумма d │ выборки лямбда │ выборки лямбда │
│ │ │ │
│ ├───────┬──────┬───────┬───────┬────────┬───────┼───────┬────────┬───────┬───────┬────────┬───────┤
│ │ 0,0 │ 0,1 │ 0,2 │ 0,3 │ 0,4 │ 0,5 │ 0,0 │ 0,1 │ 0,2 │ 0,3 │ 0,4 │ 0,5 │
├─────────┼───────┼──────┼───────┼───────┼────────┼───────┼───────┼────────┼───────┼───────┼────────┼───────┤
│ 1 │ 19,5 │ 10,8 │ 4,55 │ 3,21 │ 3,04 │ 2,84 │ 40 │ 26 │ 18 │ 15 │ 12 │ 10 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 2 │ 5,63 │ 3,72 │ 2,87 │ 2,51 │ 2,20 │ 2,11 │ 8,26 │ 4,51 │ 3,22 │ 2,82 │ 2,71 │ 2,63 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 3 │ 3,66 │ 2,83 │ 2,42 │ 2,12 │ 2,05 │ 1,94 │ 4,84 │ 3,71 │ 2,95 │ 2,73 │ 2,62 │ 2,52 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 4 │ 2,93 │ 2,31 │ 2,04 │ 1,94 │ 1,80 │ 1,78 │ 3,67 │ 3,12 │ 2,68 │ 2,50 │ 2,45 │ 2,40 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 5 │ 2,54 │ 2,!0 │ 1,87 │ 1,78 │ 1,67 │ 1,64 │ 3,08 │ 2,87 │ 2,50 │ 2,38 │ 2,34 │ 2,30 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 6 │ 2,29 │ 2,04 │ 1,82 │ 1,72 │ 1,64 │ 1,58 │ 2,73 │ 2,68 │ 2,45 │ 2,28 │ 2,22 │ 2,20 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 7 │ 2,13 │ 1,92 │ 1,78 │ 1,68 │ 1,58 │ 1,54 │ 2,49 │ 2,37 │ 2,26 │ 2,17 │ 2,10 │ 2,09 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 8 │ 2,01 │ 1,85 │ 1,74 │ 1,63 │ 1,55 │ 1,49 │ 2,31 │ 2,25 │ 2,20 │ 2,08 │ 1,96 │ 1,94 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 9 │ 1,91 │ 1,78 │ 1,67 │ 1,58 │ 1,50 │ 1,46 │ 2,19 │ 2,06 │ 1,97 │ 1,88 │ 1,78 │ 1,75 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 10 │ 1,83 │ 1,70 │ 1,62 │ 1,54 │ 1,47 │ 1,43 │ 2,08 │ 1,96 │ 1,85 │ 1,76 │ 1,56 │ 1,60 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 11 │ 1,78 │ 1,66 │ 1,57 │ 1,50 │ 1,40 │ 1,40 │ 2,00 │ 1,91 │ 1,81 │ 1,72 │ 1,63 │ 1,57 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 12 │ 1,73 │ 1,62 │ 1,53 │ 1,46 │ 1,42 │ 1,38 │ 1,93 │ 1,84 │ 1,77 │ 1,59 │ 1,60 │ 1,54 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 13 │ 1,69 │ 1,59 │ 1,50 │ 1,43 │ 1,39 │ 1,36 │ 1,88 │ 1,80 │ 1,73 │ 1,66 │ 1,57 │ 1,52 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 14 │ 1,65 │ 1,54 │ 1,45 │ 1,40 │ 1,37 │ 1,35 │ 1,83 │ 1,76 │ 1,69 │ 1,63 │ 1,54 │ 1,49 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 15 │ 1,62 │ 1,49 │ 1,41 │ 1,37 │ 1,35 │ 1,34 │ 1,78 │ 1,72 │ 1,65 │ 1,60 │ 1,52 │ 1,47 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 20 │ 1,5! │ 1,44 │ 1,36 │ 1,32 │ 1,30 │ 1,28 │ 1,64 │ 1,59 │ 1,54 │ 1,47 │ 1,44 │ 1,40 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 25 │ 1,44 │ 1,37 │ 1,30 │ 1,27 │ 1,26 │ 1,25 │ 1,55 │ 1,51 │ 1,45 │ 1,42 │ 1,39 │ 1,36 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 30 │ 1,39 │ 1,32 │ 1,27 │ 1,25 │ 1,24 │ 1,23 │ 1,48 │ 1,45 │ 1,42 │ 1,40 │ 1,34 │ 1,33 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 40 │ 1,32 │ 1,26 │ 1,24 │ 1,22 │ 1,21 │ 1,20 │ 1,40 │ 1,37 │ 1,34 │ 1,30 │ 1,28 │ 1,25 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 50 │ 1,28 │ 1,24 │ 1,22 │ 1,20 │ 1,19 │ 1,18 │ 1,35 │ 1,32 │ 1,30 │ 1,23 │ 1,26 │ 1,22 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 60 │ 1,25 │ 1,23 │ 1,21 │ 1,20 │ 1,18 │ 1,17 │ 1,31 │ 1,29 │ 1,27 │ 1,25 │ 1,23 │ 1,20 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 80 │ 1,21 │ 1,19 │ 1,17 │ 1,16 │ 1,15 │ 1,14 │ 1,26 │ 1,24 │ 1 22 │ 1,20 │ 1,19 │ 1,13 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 100 │ 1,19 │ 1,17 │ 1,15 │ 1,13 │ 1,12 │ 1,12 │ 1,23 │ 1,21 │ 1,20 │ 1,18 │ 1,17 │ 1,16 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 200 │ 1,13 │ 1,12 │ 1,12 │ 1,11 │ 1,10 │ 1,10 │ 1,16 │ 1,16 │ 1,15 │ 1,14 │ 1,13 │ 1,12 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 300 │ 1,10 │ 1,10 │ 1,09 │ 1,09 │ 1,08 │ 1,08 │ 1,12 │ 1,12 │ 1,11 │ 1,10 │ 1,10 │ 1,09 │
└─────────┴───────┴──────┴───────┴───────┴────────┴───────┴───────┴────────┴───────┴───────┴────────┴───────┘

Таблица 3

Значения коэффициента К_2

┌─────────┬──────────────────────────────────────────────┬──────────────────────────────────────────────────┐
│Суммарное│ Значения коэффициента К_2 при доверительной │ Значения коэффициента К_2 при доверительной │
│ число │ вероятности ню=0,90 и среднем относительном │вероятности ню=0,95 и среднем относительном объеме│
│дефектных│ объеме │ _ │
│ изделий │ _ │ выборки лямбда │
│ Сумма d │ выборки лямбда │ │
│ │ │ │
│ ├───────┬──────┬───────┬───────┬────────┬──────┼────────┬────────┬───────┬───────┬───────┬────────┤
│ │ 0,0 │ 0,1 │ 0,2 │ 0,3 │ 0,4 │ 0,5 │ 0,0 │ 0,1 │ 0,2 │ 0,3 │ 0,4 │ 0,5 │
├─────────┼───────┼──────┼───────┼───────┼────────┼──────┼────────┼────────┼───────┼───────┼───────┼────────┤
│ 1 │ 0,21 │ 0,24 │ 0,26 │ 0,28 │ 0,30 │ 0,33 │ 0,15 │ 0,17 │ 0,19 │ 0,21 │ 0,24 │ 0,27 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 2 │ 0,32 │ 0,34 │ 0,36 │ 0,38 │ 0,40 │ 0,42 │ 0,25 │ 0,27 │ 0,29 │ 0,31 │ 0,34 │ 0,35 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 3 │ 0,39 │ 0,41 │ 0,43 │ 0,45 │ 0,47 │ 0,48 │ 0,31 │ 0,33 │ 0,36 │ 0,39 │ 0,42 │ 0,43 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 4 │ 0,44 │ 0,43 │ 0,48 │ 0,50 │ 0,52 │ 0,54 │ 0,33 │ 0,36 │ 0,39 │ 0,42 │ 0,46 │ 0,48 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 5 │ 0,48 │ 0,50 │ 0,52 │ 0,54 │ 0,58 │ 0,61 │ 0,38 │ 0,39 │ 0,41 │ 0,45 │ 0,49 │ 0,53 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 6 │ 0,51 │ 0,53 │ 0,55 │ 0,58 │ 0,61 │ 0,64 │ 0,41 │ 0,42 │ 0,44 │ 0,47 │ 0,51 │ 0,55 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 7 │ 0,53 │ 0,55 │ 0,58 │ 0,61 │ 0,64 │ 0,67 │ 0,44 │ 0,46 │ 0,47 │ 0,49 │ 0,53 │ 0,57 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 8 │ 0,55 │ 0,57 │ 0,60 │ 0,63 │ 0,66 │ 0,69 │ 0,47 │ 0,48 │ 0,49 │ 0,52 │ 0,55 │ 0,59 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 9 │ 0,57 │ 0,59 │ 0,61 │ 0,64 │ 0,67 │ 0,71 │ 0,50 │ 0,50 │ 0,52 │ 0,55 │ 0,58 │ 0,61 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 10 │ 0,59 │ 0,61 │ 0,63 │ 0,65 │ 0,68 │ 0,72 │ 0,52 │ 0,52 │ 0,54 │ 0,57 │ 0,60 │ 0,64 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 11 │ 0,60 │ 0,62 │ 0,64 │ 0,66 │ 0,69 │ 0,72 │ 0,53 │ 0,54 │ 0,56 │ 0,50 │ 0,62 │ 0,65 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 12 │ 0,62 │ 0,64 │ 0,66 │ 0,68 │ 0,70 │ 0,73 │ 0,54 │ 0,55 │ 0,57 │ 0,60 │ 0,63 │ 0,66 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 13 │ 0,63 │ 0,65 │ 0,67 │ 0,69 │ 0,71 │ 0,73 │ 0,55 │ 0,57 │ 0,53 │ 0,61 │ 0,64 │ 0,67 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 14 │ 0,64 │ 0,66 │ 0,68 │ 0,70 │ 0,72 │ 0,74 │ 0,56 │ 0,58 │ 0,60 │ 0,62 │ 0,65 │ 0,68 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 15 │ 0,65 │ 0,65 │ 0,68 │ 0,70 │ 0,72 │ 0,74 │ 0,58 │ 0,59 │ 0,61 │ 0,63 │ 0,66 │ 0,69 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 20 │ 0,69 │ 0,71 │ 0,73 │ 0,75 │ 0,77 │ 0,79 │ 0,62 │ 0,63 │ 0,65 │ 0,67 │ 0,70 │ 0,74 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 25 │ 0,72 │ 0,73 │ 0,75 │ 0,76 │ 0,78 │ 0,80 │ 0,66 │ 0,67 │ 0,69 │ 0,71 │ 0,74 │ 0,77 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 30 │ 0,74 │ 0,74 │ 0,75 │ 0,76 │ 0,79 │ 0,81 │ 0,68 │ 0,69 │ 0,71 │ 0,73 │ 0,75 │ 0,77 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 40 │ 0,77 │ 0,77 │ 0,78 │ 0,80 │ 0,82 │ 0,84 │ 0,73 │ 0,73 │ 0,74 │ 0,76 │ 0,78 │ 0,80 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 50 │ 0,79 │ 0,79 │ 0,80 │ 0,82 │ 0,84 │ 0,85 │ 0,75 │ 0,75 │ 0,76 │ 0,78 │ 0,80 │ 0,82 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 60 │ 0,81 │ 0,82 │ 0,83 │ 0,84 │ 0,85 │ 0,86 │ 0,78 │ 0,78 │ 0,79 │ 0,80 │ 0,81 │ 0,83 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 80 │ 0,83 │ 0,84 │ 0,85 │ 0,86 │ 0,87 │ 0,88 │ 0,80 │ 0,81 │ 0,82 │ 0,83 │ 0,84 │ 0,85 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 100 │ 0,85 │ 0,85 │ 0,86 │ 0,87 │ 0,88 │ 0,89 │ 0,82 │ 0,82 │ 0,83 │ 0,84 │ 0,85 │ 0,86 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 200 │ 0,89 │ 0,89 │ 0,89 │ 0,90 │ 0,91 │ 0,92 │ 0,87 │ 0,88 │ 0,89 │ 0,89 │ 0,90 │ 0,90 │
│ │ │ │ │ │ │ │ │ │ │ │ │ │
│ 300 │ 0,95 │ 0,95 │ 0,96 │ 0,96 │ 0,96 │ 0,95 │ 0,89 │ 0,89 │ 0,90 │ 0,90 │ 0,91 │ 0,91 │
│ │ │ │ │ │ │ │ │ │ │ │ 1 │ │
└─────────┴───────┴──────┴───────┴───────┴────────┴──────┴────────┴────────┴───────┴───────┴───────┴────────┘

Таблица 4

Значения коэффициента l_0

Уровень доверительной вероятности ню	Значения коэффициента l_0 при суммарном числе партий s
	10	30	50	100	200	300
0,90	4,0	4,4	4,9	5,5	6,4	6,7
0,95	5,4	5,8	6,6	7,3	8,2	8,8

Таблица 5

Значения коэффициента l_1

Число выборок, у которых d=1	Значения коэффициента l_1 при доверительной вероятности ню=0,90 и числе партий s							Значения коэффициента l_1 при доверительной вероятности ню=0,95 и числе партий s
	19	30	50	100	200	300	10		30	50	100	200	300
4	0,00	0,00	0,00	0,00	0,00	0,00	0,00		0,00	0,00	0,00	0,00	0,00
5	0,10	0,04	0,00	0,00	0,00	0,00	0,01		0,00	0,00	0,00	0,00	0,00
6	0,18	0,13	0,10	0,08	0,01	0,00	0,03		0,01	0,00	0,00	0,00	0,00
7	0,23	0,19	0,16	0,09	0,04	0,01	0,14		0,03	0,01	0,00	0,00	0,00
3	0,28	0,25	0,23	0,19	0,14	0,09	0,15		0,12	0,09	0,01	0,00	0,00
9	0,33	0,2Э	0,27	0,23	0.20	0,17	0,22		0,19	0,16	0,03	0,02	0,00
10	0,36	0,33	0,31	0,29	0,25	0,22	0,24		0,22	0,20	0,16	0,12	0,10
11	-	0,36	0,34	0,33	0,29	0,26	-		0,25	0,23	0,20	0,18	0,16
12	-	0,38	0,37	0,35	0,32	0,30	-		0,28	0,26	0,24	0,22	0,20
13	-	0,41	0,40	0,38	0,35	0,33	-		0,31	0,29	0,28	0,26	0,24
14	-	0,43	0,42	0,40	0,38	0,36	-		0,34	0,32	0,31	0,29	0,28
15	-	0,45	0,44	0,43	0,41	0,39	-		0,36	0,35	0,32	0,30	0,29
16	-	0,47	0,46	0,44	0,43	0,41	-		0,38	0,37	0,36	0,35	0,32
17	-	0,49	0,48	0,47	0,45	0,43	-		0,40	0,39	0,38	0,37	0,36
18	-	0,50	0,49	0,48	0,46	0,45	-		0,42	0,41	0,40	0,39	0,39
19	-	0,51	0,51	0,49	0,48	0,46	-		0,43	0,42	0,42	0,42	0,41
20	-	0,52	0,52	0,51	0,49	0,48	-		0,44	0,43	0,42	0,41	0,41
40	-	0,66	0,66	0,66	0,65	0,64	-		0,59	0,58	0,58	0,57	0,57
60	-	-	0,72	0,72	0,71	0,70	-		-	0,66	0,65	0,65	0,65
80	-	-	-	0,75	0,75	0,75	-		-	-	0,70	0,70	0,70
100	-	-	-	0,76	0,76	0,76	-		-	-	0,74	0,74	0,73

Таблица 6

Значения коэффициента l_2

Число выборок, у которых d=1	Значения коэффициента l_2 при доверительной вероятности ню=0,90 и числе партий s						Значения коэффициента l_2 при доверительной вероятности ню=0,95 в числе партий s
	10	30	50	100	200	300	10	30	50	100	200	300
1	5,94	5,31	6,72	7,35	7,73	8,12	7,42	8,02	8,52	9,00	9,50	10,2
2	3,75	3,98	4,11	4,35	4,65	4,85	4,71	4,87	5,03	5,32	5,61	5,90
3	3,04	3,12	3,24	3,36	3,54	3,66	3,72	3,81	3,91	4,11	4,27	4,42
4	2,68	2,74	2,80	2,87	3,04	3,12	3,21	3,29	3,36	3,44	3,51	3,61
5	2,42	2,48	2,54	2,60	2,68	2,78	2,81	2,88	2,95	3,02	3,11	3,20
6	2,26	2,30	2,33	2,38	2,45	2,53	2,61	2,67	2,73	2,80	2,85	2,92
7	2,14	2,18	2,21	2 24	2,28	2,33	2,42	2,47	2,52	2,58	2,63	2,70
8	2,04	2,07	2,10	2,15	2,19	2,22	2,36	2,40	2,44	2,33	2,48	2,53
9	1,95	2,00	2,03	2,07	2,10	2,14	2,23	2,25	2,29	2,32	2,35	2,42
10	1,90	1,92	1,95	1,97	2,00	2,04	2,16	2,19	2,21	2,24	2,27	2,30
11	-	1,88	1,89	1,90	1,93	1,97	-	2,12	2,14	2,16	2,19	2,23
12	-	1,84	1,85	1,86	1,89	1,92	-	2,07	2,09	2,11	2,14	2,16
13	-	1,79	1,80	1,81	1,83	1,87	-	2,02	2,04	2,05	2,07	2,10
14	-	1,75	1,76	1,78	1,80	1,82	-	1,96	1,96	1,97	2,00	2,04
15	-	1,73	1,74	1,75	1,76	1,78	-	1,92	1,92	1,93	1,95	1,98
16	-	1,70	1,70	1,72	1,73	1,74	-	1,88	1,89	1,90	1,92	1,93
17	-	1,66	1,67	1,69	1,71	1,73	-	1,82	1,83	1,84	1,85	1,86
18	-	1,04	1,55	1,65	1,66	1,69	-	1,80	1,81	1,82	1,83	1,81
19	-	1,63	1,64	1,65	1,66	1,67	-	1,78	1,79	1,80	1,82	1,83
20	-	1,61	1,61	1,62	1,63	1,64	-	1,76	1,77	1,79	1,81	1,83
40	-	1,41	1,41	1,41	1,42	1,42	-	1,51	1,52	1,52	1,53	1,53
60	-	-	1,32	1,32	1,33	1,34	-	-	1,41	1,41	1,42	1,42
80	-	-	-	1,26	1,27	1,28	-	-	-	1,36	1,36	1,36
100	-	-	-	1,25	1,25	1,26	-	-	-	1,30	1,30	1,30

Таблица 7

Значения коэффициента омега(2)

Целая часть значения коэффициента а_2	Значения коэффициента омега (2) при значениях коэффициента а_2, взятых с точностью до первого знака после запятой
	0	1	2	3	4	5	6	7	8	9
0,	1,00	1,00	1,00	0,99	0,99	0,98	0,97	0,96	0,95	0,94
1,	0,92	0,91	0,89	0,87	0,85	0,83	0,81	0,80	0,78	0,75
2,	0,72	0,70	0,68	0,66	0,63	0,61	0,59	0,56	0,54	0,52
3,	0,50	0,47	0,45	0,43	0,41	0,39	0,37	0,36	0,34	0,32
4,	0,30	0,29	0,27	0,25	0,24	0,23	0,22	0,19	0,19	0,18
5,	0,17	0,16	0,15	0,14	0,13	0,12	0,12	0,11	0,10	0,10
6,	0,09	0,08	0,08	0,07	0,07	0,06	0,06	0,06	0,05	0,05
7,	0,04	0,04	0,04	0,04	0,03	0,03	0,03	0,02	0,02	0,02
8,	0,02	0,02	0,02	0,02	0,02	0,01	0,01	0,01	0,01	0,01
9,	0,01	0,01	0,01	0,01	0,01	0,01	0,01	0,01	0,01	0,00

Приложение 4
Справочное

Таблицы оперативных характеристик для объемов выборки, равных 10 и 15

Настоящим стандартом планы с объемом выборки, меньшим 20, не предусмотрены. Если по каким-либо причинам контроль проводится при объеме выборки, равном 10 или 15, то данные таблиц, приведенных ниже, дадут возможность построить оперативные характеристики планов контроля и оценить величины рисков потребления и поставщика.

Таблица 1

Квантили оперативных характеристик, в процентах, при объеме выборки, равном 10

лямбда	0,50	0,45	0,40	0,35	0,30	0,25	0,20	0,15	0,10	0,05	0,00
q_0,95	0,38	0,40	0,41	0,43	0,44	0,46	0,47	0,48	0,49	0,50	0,51
q_0,90	0,78	0,81	0,84	0,87	0,90	0,93	0,95	0,98	1,00	1,03	1,05
q_0,80	1,65	1,71	1,77	1,83	1,89	1,95	2,00	2,06	2,11	2,16	2,21
q_0,50	5,00	5,19	5,38	5,56	5,73	5,90	6,07	6,23	6,39	6,54	6,70
q_0,20	11,08	11,52	11,93	12,33	12,73	13,11	13,48	13,84	14,19	14,54	14,70
q_0,10	15,32	15,91	16,50	17,05	17,60	18,13	18,65	19,14	19,63	20,11	20,53
q_0,05	19,24	19,99	20,74	21,44	22,13	22,80	23,46	24,09	24,71	25,31	25,89
q_L	2,73	2,84	2,95	3,06	3,16	3,26	3,36	3,46	3,55	3,64	3,73

Таблица 2

Квантили оперативных характеристик, в процентах, при объеме выборки, равном 15

лямбда	0,50	0,45	0,40	0,35	0,30	0,25	0,20	0,15	0,10	0,05	0,00
q_0,95	0,25	0,26	0,27	0,28	0,29	0,30	0,31	0,32	0,33	0,33	0,34
q_0,90	0,52	0,54	0,56	0,58	0,60	0,62	0,63	0,65	0,66	0,68	0,70
q_0,80	1,09	1,14	1,18	1,22	1,26	1,30	1,33	1,37	1,41	1,44	1,48
q_0,50	3,35	3,48	3,60	3,72	3,84	3,96	4,08	4,19	4,30	4,41	4,52
q_0,20	7,50	7,80	8,10	8,38	8,66	8,93	9,19	9,41	9,62	9,93	10,19
q_0,10	10,51	10,93	11,34	11,73	12,11	12,49	12,86	13,22	13,57	13,91	14,25
q_0,05	13,34	13,88	14,42	14,92	15,42	15,89	16,36	16,81	17,26	17,70	18,10
q_L	1,80	1,88	1,95	2,02	2,09	2,16	2,22	2,29	2,35	2,41	2,47

Приложение 5
Рекомендуемое

Некоторые практические применения последующих оценок, оперативных характеристик и предела среднего уровня выходного качества

1. Применение последующих оценок

1.1. Последующие оценки среднего уровня входного качества следует применять в тех случаях, когда решения, перечисленные в п. 5.1.2 настоящего стандарта, принимаются на основе информации о качестве продукции, поступающей на контроль.

Последующие оценки среднего уровня выходного качества следует применять в тех случаях, когда решения, перечисленные в п. 5.1.2 настоящего стандарта, принимаются на основе информации о качестве продукции, прошедшей контроль.

Примечание. Последующие оценки могут вычисляться по методике разд. 5 настоящего стандарта или настоящего приложения, а также по результатам сплошного контроля ряда партий.

1.2. Последующие оценки средних уровней входного и выходного качества следует применять одновременно:

- при контроле потребителем полученной продукции;