Значение момента инерции 
определяют как сумму моментов инерции 
отдельных участков расчетного контура поперечного сечения относительно центральных осей, проходящих через центр тяжести расчетного контура.
определяют как сумму моментов инерции отдельных участков расчетного контура поперечного сечения относительно центральных осей, проходящих через центр тяжести расчетного контура. Положение центра тяжести расчетного контура относительно выбранной оси определяют по формуле
, (6.110) где 
- длина отдельного участка расчетного контура;
- длина отдельного участка расчетного контура;
- расстояние от центров тяжести отдельных участков расчетного контура до выбранных осей. Для замкнутого прямоугольного контура (рисунок 6.12, а, г) с длиной участков 
и 
в направлении осей Х и Y центр тяжести расположен в месте пересечения осей симметрии контура.
и в направлении осей Х и Y центр тяжести расположен в месте пересечения осей симметрии контура. Значение момента инерции расчетного контура определяют по формуле
, (6.111) где 
- момент инерции участков контура длиной 
и 
относительно осей 
и 
, совпадающих с осями Y и X.
- момент инерции участков контура длиной и относительно осей и , совпадающих с осями Y и X. Значения 
определяют по формулам (6.112) и (6.113), принимая условно ширину каждого участка контура длиной 
и 
, равной единице:
определяют по формулам (6.112) и (6.113), принимая условно ширину каждого участка контура длиной и , равной единице:
; (6.112)
. (6.113) Значения 
определяют по формуле
определяют по формуле
(6.114) или
. (6.115) Для незамкнутого расчетного контура, состоящего из трех прямолинейных участков длиной 
и 
(рисунок 6.12, в), например, при расположении площадки передачи нагрузки (колонны) у края плоского элемента (плиты перекрытия), положение центра тяжести расчетного контура в направлении оси X определяют по формуле
и (рисунок 6.12, в), например, при расположении площадки передачи нагрузки (колонны) у края плоского элемента (плиты перекрытия), положение центра тяжести расчетного контура в направлении оси X определяют по формуле
, (6.116) а в направлении оси Y центр тяжести расположен по оси симметрии расчетного контура.
Значения момента инерции расчетного контура относительно центральных осей 
и 
определяют по формуле (6.111).
и определяют по формуле (6.111). Значения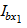 
и 
определяют по формулам:
и определяют по формулам:
; (6.117)
. (6.118) Значения 
и 
определяют по формулам:
и определяют по формулам:
; (6.119)
. (6.120) Значения 
и 
определяют по формулам:
и определяют по формулам:
и 
; (6.121)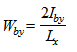
. (6.122) При расчете принимают наименьшие значения моментов сопротивления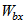 
.
. Для незамкнутого расчетного контура, состоящего из двух прямолинейных участков длиной 
и 
(рисунок 6.12, б), например при расположении площадки передачи нагрузки (колонны) вблизи угла плоского элемента (плиты перекрытия), положение центра тяжести расчетного контура в направлении осей X и Y определяют по формуле
и (рисунок 6.12, б), например при расположении площадки передачи нагрузки (колонны) вблизи угла плоского элемента (плиты перекрытия), положение центра тяжести расчетного контура в направлении осей X и Y определяют по формуле
. (6.123) Значения момента инерции расчетного контура относительно центральных осей 
и 
определяют по формуле (6.20).
и определяют по формуле (6.20). Значения 
и 
определяют по формулам:
и 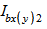определяют по формулам:
; (6.124)
; (6.125)
; (6.126)
. (6.127) Значения 
и 
определяют по формулам:
и определяют по формулам:
и 
; (6.128)
и 
. (6.129) При расчете принимают наименьшие значения моментов сопротивления 
и 
.
и . 6.2.52 Значения моментов сопротивления поперечной арматуры при продавливании 
в том случае, когда поперечная арматура расположена равномерно вдоль расчетного контура продавливания в пределах зоны, границы которой отстоят на расстоянии 
в каждую сторону от контура продавливания бетона (рисунок 6.14), принимают равными соответствующим значениям 
и 
.
в том случае, когда поперечная арматура расположена равномерно вдоль расчетного контура продавливания в пределах зоны, границы которой отстоят на расстоянии в каждую сторону от контура продавливания бетона (рисунок 6.14), принимают равными соответствующим значениям и 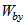. При расположении поперечной арматуры в плоском элементе сосредоточенно по осям грузовой площадки, например, по оси колонн (крестообразное расположение поперечной арматуры в перекрытии), моменты сопротивления поперечной арматуры определяют по тем же правилам, что и моменты сопротивления бетона, принимая соответствующую фактическую длину ограниченного участка расположения поперечной арматуры по расчетному контуру продавливания 
и 
(рисунок 6.12, г).
и (рисунок 6.12, г).7 Расчет элементов железобетонных конструкций по предельным состояниям второй группы
7.1 Общие положения
7.1.1 Расчеты по предельным состояниям второй группы включают:
- расчет по раскрытию трещин;
- расчет по деформациям.
7.1.2 Расчет по образованию трещин производят для проверки необходимости расчета по раскрытию трещин, а также для проверки необходимости учета трещин при расчете по деформациям.