Черт.8
Введением приведенной случайной величины для случая 
получим
получим  | |
| 219 × 69 пикс. Открыть в новом окне | |
Зависимость между объемом выборки 
и приемочным коэффициентом 
и приемочным коэффициентом  | |
| 273 × 88 пикс. Открыть в новом окне | |
и
 | |
| 231 × 88 пикс. Открыть в новом окне | |
откуда
 | |
| 245 × 51 пикс. Открыть в новом окне | |
и
 | |
| 248 × 59 пикс. Открыть в новом окне | |
Для максимального значения среднего размаха получим
, (33) а для допускаемого значения среднего размаха
, (34) где
. (35)
 | |
| 267 × 52 пикс. Открыть в новом окне | |
Приемочная трапеция определена значениями 
, 
, 
, 
и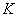 
(черт.9). С помощью приемочной трапеции можно установить, что для партии объемом 
счетчиков условия
, , , и (черт.9). С помощью приемочной трапеции можно установить, что для партии объемом счетчиков условия 
; 
; 
(36) выполняются в том случае, если
; 
(37) или, записав в другой форме
; 
, (38) чем выражается, что точка, характеризующаяся значениями 
и 
, находится в пределах приемочной трапеции (черт.9).
и , находится в пределах приемочной трапеции (черт.9).  | |
| 160 × 327 пикс. Открыть в новом окне | |
Черт.9
Пример. Если приемочный уровень дефектности 
=1% (0,01), браковочный уровень дефектности 
=6,8% (0,068), риск изготовителя 
=5,5% (0,055), риск потребителя 
=10% (0,1), то соответствующие им значения приведенной случайной величины, взятые из статистических таблиц, составляют: 
=2,33;
=1% (0,01), браковочный уровень дефектности =6,8% (0,068), риск изготовителя =5,5% (0,055), риск потребителя =10% (0,1), то соответствующие им значения приведенной случайной величины, взятые из статистических таблиц, составляют: =2,33; 
*=1,49; 
=1,60; 
=1,28; 
=2,58; 
=1,83. Для 
=5 
=2,326, 
=0,864.
=5 =2,326, =0,864. Исходя из указанных значений, получим:
=0,80; 
; =40,1;
=0,93; 
. 6. Условия приемки при контроле по количественному признаку, основанные на с.к.о. выборки
Метод среднеквадратического отклонения выборки основан на анализе с.к.о. выборки 
и оценки 
, определяемой зависимостью
и оценки , определяемой зависимостью 
, (39) где
. (40) Приемочный коэффициент 
определяется зависимостью
определяется зависимостью  | |
| 228 × 52 пикс. Открыть в новом окне | |
а объем выборки
 | |
| 208 × 59 пикс. Открыть в новом окне | |
Допускаемое значение среднеквадратического отклонения выборки
, (43) где
. (44)
 | |
| 257 × 52 пикс. Открыть в новом окне | |