Государственный стандарт РФ ГОСТ Р ИСО 5725-4-2002"Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений"(принят и введен в действие постановлением Госстан стр. 3

a) характеристики стабильны - в каких бы то ни было мерах предосторожности нет необходимости;

b) аттестованное значение характеристики может изменяться в зависимости от условий хранении: контейнер должен храниться как до, так и после его открытия таким образом, как это описано в аттестате на стандартный образец;

c) характеристики изменяются по времени по известному закону: представляется аттестат, содержащий аттестованное значение характеристики, установленное в определенное время.

4.2.1.4 Возможное различие между аттестованным и истинным значением, выраженное через неопределенность стандартного образца (см. Руководство ИСО 35 [2]), в методах, приводимых в настоящем стандарте, не принимают во внимание.

4.2.2 Проверка и распределение стандартного образца

В случаях, когда перед распределением происходит разделение единицы стандартного образца, это должно выполняться осторожно, чтобы избежать внесения какой-либо дополнительной погрешности. Для справок следует воспользоваться соответствующими международными стандартами по разделению (разделу) проб. Единицы стандартных образцов для распределения должны отбираться по случайному принципу. Если имеет место неразрушающий измерительный контроль, возможно предоставить всем лабораториям, участвующим в межлабораторном эксперименте, одну и ту же единицу стандартного образца, однако это увеличит продолжительность эксперимента.

4.3 Основные требования к схемам организации эксперимента по оценке систематической погрешности метода измерений

4.3.1 Целью эксперимента является оценка значения систематической погрешности метода измерений и установление, является ли она статистически значимой. Если установлено, что систематическая погрешность не является статистически значимой, то целью является определение значения максимальной систематической погрешности, которая могла бы, с определенной вероятностью, оставаться цеобнаруживаемой в результатах эксперимента.

4.3.2 Программа эксперимента - аналогична программе эксперимента по оценке прецизионности, описанного в 4.1 ГОСТ Р ИСО 5725-2. Различия заключаются в следующем:

a) существует дополнительное требование к использованию принятого опорного значения и

b) количество участвующих лабораторий и число результатов измерений должны также удовлетворять требованиям 4,5.

4.4 Ссылки на ГОСТ Р ИСО 5725-1 и ГОСТ Р ИСО 5725-2

Используют раздел 6 ГОСТ Р ИСО 5725-1 и разделы 5 и 6 ГОСТ Р ИСО 5725-2. При чтении частей 1 и 2 ГОСТ Р ИСО 5725 в контексте части 4 вместо терминов "прецизионность" или "повторяемость и воспроизводимость" следует употреблять термин "правильность".

4.5 Необходимое количество лабораторий

Количество лабораторий и результатов измерений, требующихся на каждом уровне, взаимозависимы. Необходимое количество лабораторий рассматривают в 6.3 ГОСТ Р ИСО 5725-1. Указания в отношении их количества, приведены ниже.

Для того, чтобы в результате эксперимента можно было достаточно надежно оценить систематическую погрешность метода (см. приложение С), минимальное количество лабораторий р и результатов измерений n должно удовлетворять следующему неравенству

где - заданное значение систематической погрешности, которое участник эксперимента желает обнаружить в результатах эксперимента;

- стандартное отклонение воспроизводимости метода измерений.

А как функция p и n задается следующим выражением

где ; (7)

- стандартное отклонение повторяемости метода измерений.

Значения А представлены в таблице 1.

В идеальном случае выбор сочетания количества лабораторий и повторно получаемых результатов измерений на лабораторию должен удовлетворять требованию, описанному уравнением (5) при значении , задаваемом экспериментатором. Однако из практических соображений выбор количества лабораторий обычно представляет собой компромисс между наличием ресурсов и желанием снизить значение до удовлетворительного уровня. Если воспроизводимость метода измерений невысока, то тогда практически невозможно будет достигнуть высокой степени определенности при оценке систематической погрешности. Когда , (то есть > 1), как это часто происходит, получением более чем двух результатов измерений на лабораторию из расчета на уровень мало чего можно достичь.

Таблица 1 - Значения неопределенности оценки систематической погрешности метода измерений

р	= 1			= 2			= 5
	n = 2	n = 3	n = 4	n = 2	n = 3	n = 4	n = 2	n = 3	n = 4
5	0,62	0,51	0,44	0,82	0,80	0,79	0,87	0,86	0,86
10	0,44	0,36	0,31	0,58	0,57	0,56	0,61	0,61	0,61
15	0,36	0,29	0,25	0,47	0,46	0,46	0,50	0,50	0,50
20	0,31	0,25	0,22	0,41	0,40	0,40	0,43	0,43	0,43
25	0,28	0,23	0,20	0,37	0,36	0,35	0,39	0,39	0,39
30	0,25	0,21	0,18	0,33	0,33	0,32	0,35	0,35	0,35
35	0,23	0,19	0,17	0,31	0,30	0,30	0,33	0,33	0,33
40	0,22	0,18	0,15	0,29	0,28	0,28	0,31	0,31	0,31

4.6 Статистическая оценка

Результаты измерений должны быть обработаны согласно ГОСТ Р ИСО 5725-2. В частости, если выявляются выбросы, должны быть предприняты необходимые меры, чтобы изучить причины их появления, включая переоценку соответствия принятого опорного значения.

4.7 Интерпретация результатов статистической оценки

4.7.1 Проверка прецизионности

Прецизионность метода измерений выражают через (оценку стандартного отклонения повторяемости) и (оценку стандартного отклонения воспроизводимости). В равенствах (8) - (10) принято допущение, заключающееся в равном количестве (n) результатов измерений в каждой лаборатории. Если это условие не соблюдается, то для расчета и должны быть использованы соответствующие формулы, приведенные в ГОСТ Р ИСО 5725-2.

4.7.1.1 Оценку дисперсии повторяемости для участвующих в эксперименте лабораторий рассчитывают следующим образом

где и - соответственно дисперсия и среднее значение n результатов измерений , полученных в лаборатории i.

Для подтверждения, что между внутрилабораторными дисперсиями не существует никаких существенных различий, к дисперсиям необходимо применить критерий Кохрена, описанный в ГОСТ Р ИСО 5725-2. С целью более тщательного исследования потенциальных выбросов должны быть также построены диаграммы Манделя h и k, приведенные в ГОСТ Р ИСО 5725-2.

Если стандартное отклонение повторяемости стандартного метода измерений ранее не было определено в соответствии с ГОСТ Р ИСО 5725-2, то будет считаться его наилучшей оценкой. Если стандартное отклонение повторяемости стандартного метода было определено в соответствии с ГОСТ Р ИСО 5725-2, то значение дисперсии может быть оценено следующим соотношением

Статистику сравнивают с критическим значением

где представляет собой (1 - ) - квантиль - распределения с v | = р(n - 1)| степенями свободы. Если не установлено иначе, то принимают равным 0,05.

a) Если , то не значимо больше ,

b) Если , то значимо больше .

В первом случае для оценки систематической погрешности и метода измерений будет использовано стандартное отклонение повторяемости . В последнем случае необходимо исследовать причины расхождения и, возможно, повторить эксперимент.

4.7.1.2 Оценку дисперсии воспроизводимости для участвующих в эксперименте лабораторий рассчитывают следующим образом

Если стандартное отклонение воспроизводимости стандартного метода измерений ранее не было определено в соответствии с ГОСТ Р ИСО 5725-2, то будет его наилучшей оценкой. Если стандартные отклонения воспроизводимости 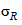и повторяемости стандартного метода измерений были определены в соответствии с ГОСТ Р ИСО 5725-2, то может быть косвенно оценено путем вычисления следующего соотношения