В.3 Оценка правильности

Правильность метода измерений была оценена путем расчета 95%-ных доверительных интервалов систематической погрешности метода с использованием соотношения (19) и определения положения этих интервалов относительно нуля (таблица В.5). Поскольку на уровнях 3 - 5 эти доверительные интервалы охватывают нулевое значение, систематическая погрешность данного метода измерений не является значимой на уровнях высоких концентраций марганца 3 - 5; поскольку на уровнях 1 и 2 доверительные интервалы не охватывают нулевого значения, систематическая погрешность является значимой на уровнях низких концентраций 1 и 2.

В.4 Дальнейший анализ

Из исходных данных может быть получена более подробная информация посредством выполнения дополнительного анализа, такого как регрессионный анализ для в функции от .

Таблица B.1 Содержание марганца в железных рудах. Принятые опорные значения

Уровень	1	2	3	4	5
Принятое опорное, значение , % Mn	0,010 0	0,093 0	0,401 0	0,777 0	2,530 0

Таблица В.2 - Содержание марганца в железных рудах. Результаты анализа, в процентах Mn

Номер лаборатории	Номер колбы	Уровень
		1		2		3		4			5
1	1	0,0118	0,0121	0,0880	0,0875	0,408	0,407	0,791	0,791	2,584		2,560
	2	0,0121	0,0121	0,0865	0,0867	0,407	0,408	0,794	0,801	2,535		2,545
2	1	0,0131	0,0115	0,0894	0,0861	0,411	0,405	0,760	0,766	2,543		2,591
	2	0,0115	0,0115	0,0887	0,0867	0,406	0,399	0,766	0,783	2,516		2,567
3	1	0,0118	0,0112	0,0864	0,0849	0,410	0,403	0,752	0,767	2,526		2,463
	2	0,0110	0,0104	0,0867	0,0896	0,408	0,400	0,755	0,753	2,515		2,493
4	1	0,0107	0,0121	0,0881	0,0892	0,402	0,402	0,780	0,750	2,560		2,520
	2	0,0114	0,0121	0,0861	0,0874	0,404	0,402	0,777	0,750	2,600		2,520
5	1	0,0120	0,0128	0,0904	0,0904	0,404	0,400	0,775	0,775	2,470		2,510
	2	0,0112	0,0128	0,0862	0,0870	0,404	0,396	0,770	0,780	2,500		2,480
6	1	0,0111	0,0110	0,0892	0,0893	0,402	0,398	0,786	0,782	2,531		2,514
	2	0,0110	0,0111	0,0900	0,0864	0,408	0,404	0,780	0,772	2,524		2,494
7	1	0,0088	0,0095	0,0893	0,0895	0,390	0,390	0,754	0,762	2,510		2,521
	2	0,0070	0,0086	0,0859	0,0886	0,395	0,395	0,758	0,756	2,500		2,513
8	1	0,0115	0,0112	0,0823	0,0823	0,390	0,396	0,761	0,765	2,501		2,499
	2	0,0113	0,0113	0,0828	0,0829	0,400	0,389	0,770	0,766	2,507		2,490
9	1	0,0123	0,0120	0,0862	0,0866	0,414	0,414	0,765	0.765	2,523		2,520
	2	0,0117	0,0118	0,0865	0,0876	0,411	0,414	0,765	0,765	2,521		2,508
10	1	0,0095	0,0086	0,0780	0,0720	0,390	0,370	0,746	0,730	2,530		2,580
	2	0,0092	0,0084	0,0780	0,0730	0,392	0,374	0,750	0,738	2,510		2,610
11	1	0,0125	0,0125	0,0900	0,0890	0,405	0,395	0,790	0,780		2,520		2,520
	2	0,0130	0,0125	0,0890	0,0895	0,400	0,405	0,785	0,790		2,530		2,520
12	1	0,0125	0,0130	0,0885	0,0890	0,405	0,395	0,790	0,780		2,535		2,525
	2	0,0115	0,0130	0,0890	0,0875	0,405	0,390	0,775	0,790		2,550		2,495
13	1	0,0125	0,0116	0,0842	0,0832	0,399	0,399	0,784	0,777		2,523		2,523
	2	0,0121	0,0116	0,0832	0,0828	0,398	0,399	0,782	0,777		2,527		2,537
14	1	0,0116	0,0120	0,0898	0,0890	0,418	0,416	0,797	0,800		2,602		2,602
	2	0,0098	0,0116	0,0900	0,0902	0,415	0,415	0.801	0,790		2,592		2,602
15	1	0,0108	0,0112	0,0871	0,0860	0,399	0,400	0,775	0,774		2,488		2,495
	2	0,0112	0,0111	0,0883	0,0861	0,397	0,401	0,783	0,773		2,503		2,485
16	1	0,0109	0,0108	0,0846	0,0858	0,392	0,400	0,779	0,769		2,528		2,516
	2	0,0111	0,0110	0,0849	0,0855	0,396	0,397	0,751	0,753		2,528		2,525
17	1	0,0100	0,0110	0,0849	0,0880	0,409	0,410	0,766	0,794		2,571		2,380
	2	0,0100	0,0100	0,0830	0,0890	0,392	0,402	0,755	0,775		2,429		2,488
18	1	0,0117	0,0102	0,0880	0,0881	0,405	0,404	0,771	0,773		2,520		2,511
	2	0,0125	0,0103	0,0868	0,0882	0,402	0,403	0,778	0,763		2,514		2,503
19	1	0,0099	0,0128	0,0945	0,0905	0,398	0,375	0,770	0,767		2,483		2,351
	2	0,0118	0,0128	0,0924	0,0884	0,418	0,382	0,799	0,760		2,485		2,382

Таблица В.3 Содержание марганца в железных рудах. Лабораторные средние значения и лабораторные дисперсии

Номер лаборатории	Уровень
	1	2	3	4	5
Лабораторное среднее значение
1	0,012 03	0,087 18	0,407 50	0,794 25	2,556 00
2	0,011 90	0,087 73	0,405 25	0,768 75	2,554 25
3	0,011 10	0,086 90	0,405 25	0,756 75	2,499 25
4	0,011 58	0,087 70	0,402 50	0,764 25	2,550 00
5	0,012 20	0,088 50	0,401 00	0,775 00	2,490 00
б	0,011 05	0,088 73	0,403 00	0,780 00	2,515 75
7	0,008 48	0,088 33	0,392 50	0,757 50	2,511 00
8	0,011 33	0,082 58	0,393 75	0,765 50	2,499 25
9	0,011 95	0,086 73	0,413 25	0,765 00	2,518 00
10	0,008 93	0,075 25	0,381 50	0,741 00	2,557 50
11	0,012 63	0,089 38	0,401 25	0,786 25	2,522 50
12	0,012 50	0,088 50	0,398 75	0,783 75	2,526 25
13	0,011 95	0,083 35	0,398 75	0,780 00	2,527 50
14	0,011 25	0,089 75	0,416 00	0,797 00	2,599 50
15	0,01108	0,086 88	0,399 25	0,776 25	2,492 75
16	0,010 95	0,085 20	0,396 25	0,763 00	2,524 25
17	0,010 25	0,086 23	0,403 25	0,772 50	2,467 00
18	0,011 18	0,087 78	0,403 50	0,771 25	2,512 00
19	0,011 83	0,091 45	0,393 25	0,774 00	2,425 25
Лабораторная дисперсия
1
2
3
4
5
6
7
8
9				0
10
11
12
13
14
15
16
17
18
19

Таблица В.4 - Содержание марганца в железных рудах. Выбросы и квазивыбросы

Уровень	Номер лаборатории	Вычисленная статистика*	Критическое значение статистики
Перечень выбросов ( = 0.01)
1	7	G2=0,295	G2(19)=0,339 8
	10
2	10	G1=3,305	G1(19)=2,968
3	19	C=0,474	С(4,19)=0,276
	10	С=0,305	С(4,18)=0,288
4	-	-	-
5	17	С=0,358	С(4,19)=0,276
	19	С=0,393	С(4,18)=0,288
Перечень квазивыбросов ( = 0,05)
1	-	-	-
2	-	-	-
3	-	-	-
4	-	-	-
5	10	С=0,284	С(4,17)=0,250
С - критерий Кохрена; G1 - критерий Граббса для одною выброса; G2 - критерий Граббса для двух выбросов.

Таблица В.5 - Содержание марганца в железных рудах. Оценка стандартных отклонений повторяемости, воспроизводимости и систематической погрешности метода измерений

Показатели, условные обозначения*	Уровень
	1	2	3	4	5
n	4	4	4	4	4
p	17	18	17	18	16
	0,000 65	0,001 43	0,004 07	0,008 95	0,018 15
	0,000 84	0,002 48	0,007 06	0,013 85	0,032 46
	1,29	1,73	1,73	1,54	1,79
А	0,352 8	0,399 9	0,411 7	0,383 0	0,428 7
	0,000 296	0,000 991	0,002 906	0,005 301	0,013 916
	0,011 6	0,087 4	0,402 4	0,773 9	2,524 9
	0,010 0	0,093 0	0,401 0	0,777 0	2,530 0
	0,001 6	- 0,005 6	0,001 4	- 0,003 1	- 0,005 1
	0,001 3	- 0,006 6	-0,001 5	- 0,008 4	- 0,0190
	0,001 9	- 0,004 6	0,004 3	0,002 2	0,008 8
* Условные обозначения см. в приложении А.

1845 × 1688 пикс.     Открыть в новом окне

1864 × 1651 пикс.     Открыть в новом окне

1846 × 1625 пикс.     Открыть в новом окне

1567 × 1533 пикс.     Открыть в новом окне

1857 × 1614 пикс.     Открыть в новом окне

1371 × 878 пикс.     Открыть в новом окне

1345 × 540 пикс.     Открыть в новом окне

1654 × 1103 пикс.     Открыть в новом окне

Вывод соотношений

C.I. Формулы (5) и (6) (см. 4.5)

Минимальное количество лабораторий р и результатов измерений n вычисляют, исходя из требований удовлетворения двух следующих условий:

a) измерение должно сделать возможным обнаружение, что систематическая погрешность равна нулю с вероятностью ;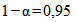

b) измерение должно сделать возможным обнаружение ожидаемого значении систематической погрешности с вероятностью .

Первое условие развито согласно 4.7.2, где доверительный интервал для систематической погрешности метода измерений использован для выполнения статистической проверки гипотезы, что систематическая погрешность равна нулю ( : 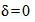), альтернативно гипотезе, что систематическая погрешность не равна нулю ( : ).

Эквивалентной формой этой проверки является сравнение абсолютного значения оценки систематической погрешности метода измерений с критическим значением К и отклонением гипотезы ( ), если (и принятием гипотезы ( ), если ).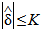

К может быть вычислена, используя требование, что вероятность отклонения гипотезы , если она истинна, должна быть равна выбранному уровню значимости :

Найдем критическое значение К на основе соотношений:

где Ф( ) - интегральная функция распределения стандартного нормального распределения;

- р-квантиль стандартного нормального распределения;

- дисперсия оценки систематической погрешности метода измерений:

где , a представляет собой межлабораторную дисперсию, так что .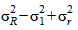

Для альтернативной гипотезы потребуем выполнения условия, при котором в результате эксперимента станет возможным определить ожидаемое значение систематической погрешности с вероятностью :

что дает