| | |
| 362 × 41 пикс. Открыть в новом окне | |
где  - сумма квадратов всех разностей δ( A− B)j
- сумма квадратов всех разностей δ( A− B)j
v= 2(20 − 1) = 38,(Е.17)
гдеv - число степеней свободы.
Экспериментальное среднеквадратическое отклонение действительно для разности вы-сот на расстоянии 60 м
 | |
| 316 × 60 пикс. Открыть в новом окне | |
 | |
| 272 × 53 пикс. Открыть в новом окне | |
где  - экспериментальное среднеквадратическое отклонение для нивелирования на 1 км двойного хода.
- экспериментальное среднеквадратическое отклонение для нивелирования на 1 км двойного хода.
Е.3.4 Статистические испытания
Е.3.4.1Статистические испытания рекомендованы только для полной методики испытаний. Для интерпретации результатов статистические испытания выполняют, используя:
-экспериментальное среднеквадратическое отклонение S разности высот;
-разность δℎ смещений нуль-точек двух нивелирных реек и её экспериментальное сред-неквадратическое отклонение Sδℎ.
Чтобы ответить на следующие вопросы (см. таблицу Е.2):
Т а б л и ц а Е.2 - Статистические испытания
 | |
| 726 × 103 пикс. Открыть в новом окне | |
а) меньше ли рассчитанное экспериментальное среднеквадратическое отклонение S значения σ, представленного изготовителем, или какого-либо другого предварительно определенного значения Snor;
б) принадлежат ли два экспериментальных среднеквадратических отклонения S и ,определенные из двух различных выборочных измерений, к одной и той же генеральной совокупности, принимая, что обе выборки имеют одно и то же число степеней свободы v; экспериментальные среднеквадратические отклонения S и получают из:
-двух выборок измерений, выполненных на одном и том же нивелире, но разными наблюдателями;
-двух выборок измерений, выполненных на одном и том же нивелире, но в разное время;
-двух выборок измерений, выполненных на разных нивелирах;
в) равна ли нулю разность δℎ смещений нуль-точек двух нивелирных реек.
Для следующих испытаний принимают доверительный уровень (1 − α) = 0,95 и согласно цели измерений число степеней свободы v= 38.
Е.3.4.2 Вопрос а)
Нуль-гипотезу, устанавливающую, что экспериментальное среднеквадратическое отклонение S меньше или равно теоретическому или предварительно определенному значению σ, не отвергают, если выполнено следующее условие
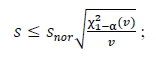 (Е.20)
(Е.20) (Е.21)
(Е.21) В противном случае нуль-гипотезу отвергают.
Е.3.4.3 Вопрос б)
В случае двух разных выборок испытание показывает, принадлежат ли экспериментальные среднеквадратические отклоненияи S и к одной и той же генеральной совокупности. Соответствующую нуль-гипотезу σ = не отвергают, если выполнено следующее условие
 | |
| 268 × 52 пикс. Открыть в новом окне | |
 | |
| 274 × 53 пикс. Открыть в новом окне | |
В противном случае нуль-гипотезу отвергают.
Е.3.4.4 Вопрос в)Гипотезу равенства средних значений δ̅ℎ1 и δ̅ℎ2 (нуль-гипотезу для δ) не отвергают, если выполнено следующее условие
| | |
| 203 × 44 пикс. Открыть в новом окне | |
В противном случае нуль-гипотезу отвергают.
Число степеней свободы и, таким образом, соответствующее число значений, полученных в испытании
(взятые из справочников по статистике) изменяются, если анализируют разное число измерений.
| | |
| 281 × 35 пикс. Открыть в новом окне | |
Е .4 Пример упрощенной методики испытаний по определению характеристики качества измерений в полевых условиях для нивелира
Е.4.1 Измерения В таблице Е.3 включены в столбцах с 1-го по 3-ий и с 7-го по 9-ый 20 отсчетов в прямом и обратном направлениях (измеренных значений ℎAj и ℎBj).
Т а б л и ц а Е.3- Измерения и разности
 | |
| 728 × 417 пикс. Открыть в новом окне | |
Е.4.2 Расчет характеристики качества измерения Измеренные разности высот ℎ1, … , ℎ20 рассчитаны в соответствии с уравнением (1) (см. столбцы 4 и 10 таблицы Е.3).
