Величина
(10.13) где λ – гибкость стержня;
(10.14)Из формулы (10.14) следует, что σкр возрастает по мере увеличения гибко-сти стержня и при достижении σ кр предела пропорциональности формула Эйлера становится неприменимой, при
(10.15)Предельная гибкость для стали λ≥ 100, в этом случае применяют формулу Ясинского:
σкр = a – b λ ,
где a, b – табличные коэффициенты, определяемые эмпирически.
Условную гибкость определяют по формуле
(10.16)10.6.6 Расчет на прочность элементов, подверженных центральному растяжению или сжатию силой Р, выполняют по формуле
(10.17) где F – площадь сечения;
R– расчетное сопротивление.
10.6.7 Расчет на устойчивость сплошностенчатых элементов, подверженных центральному сжатию, выполняют по формуле
(10.18) где φ – коэффициент продольного изгиба.
Значения φ для стали приведены в приложении Д СП 16.13330.2017, для алюминия – в приложениях Г и Е СП 128.13330.2016.
10.6.8 Расчет отдельностоящих телескопических стоек (рисунок 10.9)
Коэффициенты расчетной длины μ для нижнего участка следует прини-мать в зависимости от отношения
(10.19)а величину
(10.20)
 | |
| 263 × 62 пикс. Открыть в новом окне | |
 | |
| 231 × 200 пикс. Открыть в новом окне | |
Рисунок 10.9
Значения μ приведены в таблице И.2 приложения И СП 16.13330.2017. Коэффициент расчетной длины μ2 для верхнего элемента стойки вычисляют по формуле
(10.21) 10.6.8.1 Несущую способность стойки вычисляют по формуле
(10.22)где S – коэффициент продольной устойчивости (безопасности), равный 2,8 для стали.
10.6.8.2 Опора на стойки осуществляется через продольные балки (рисунок 10.9, б), которые устанавливают попарно при наращивании по длине. Возможна установка в опорную вилку одной балки, что приводит к возникновению эксцентриситета е. Поэтому при расчете стоек (в т. ч. стоек рам) следует вводить поправку на внецентренные нагрузки с учетом е.
Внецентренная нагрузка на стойку – обычное явление при монтаже опалубки (в т. ч. при установке продольных и поперечных балок различных ширины и характеристик).
10.8.6.3 Изгиб стойки парой сил (рисунок 10.10) Рe вызывает нормальные напряжения. 
∙ – полное напряжение.
∙ – полное напряжение.  | |
| 208 × 62 пикс. Открыть в новом окне | |
 | |
| 103 × 235 пикс. Открыть в новом окне | |
Рисунок 10.10
Для прямоугольного поперечного сечения при y = h/2
 | |
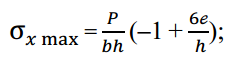| 229 × 65 пикс. Открыть в новом окне | |
 | |
| 239 × 61 пикс. Открыть в новом окне | |
При ℯ < h/6 знак напряжений не меняется, при ℯ = h/6 наибольшее сжимающее напряжение равно 2 и напряжение на противоположной стороне поперечного сечения равно нулю, при ℯ > h/6 знак напряжений меняется, тогда
 | |
| 252 × 57 пикс. Открыть в новом окне | |
Где iz– радиус инерции относительно оси Z.
Уравнение (10.26) допускается применять для других форм поперечного сечения.
При внецентренной нагрузке (рисунок 10.11)
(10.27)  | |
| 99 × 167 пикс. Открыть в новом окне | |
Рисунок 10.11
Уравнение изогнутой оси
(10.28)При увеличении Pℓ резко увеличиваются прогибы, быстрее, чем увеличивается P, и при Pℓ = π/2 прогибы = ∞.