 | |
| 658 × 427 пикс. Открыть в новом окне | |
Через точку Е, значение которой соответствует обобщенному безразмерному коэффициенту А, проводят прямую, параллельную оси ординат до пересечения в точке В с кривой, соответствующей температуре, установленной по п. 5.3.
Через точку В проводят прямую, параллельную оси абсцисс.
Через точку Е_1, значение которой соответствует обобщенному безразмерному коэффициенту А_1, восстанавливают перпендикуляр до пересечения с прямой, параллельной оси абсцисс в точке С.
Через точку С интерполируют кривую до пересечения с осью ординат, точка D.
Численное значение температуры, полученное на оси ординат в точке D, уменьшают на значение поправки (К), учитывающей неравномерность нагрева изделия, по толщине и значение поправки (K_1), учитывающей высыхание покрытия при остывании изделия после извлечения его из сушильной установки, по таблице.
 | |
| 649 × 150 пикс. Открыть в новом окне | |
5.8. Пример расчета температуры сушки изделия приведен в приложении 2.
6. Требования безопасности
6.1. При изготовлении образцов для испытаний и при проведении испытаний должны соблюдаться требования пожарной безопасности и промышленной санитарии в соответствии с требованиями ГОСТ 12.3.005-75.
6.2. Метеорологические условия и содержание вредных примесей в рабочей зоне помещений не должны превышать норм, установленных ГОСТ 12.1.005-88.
6.3. Электробезопасность при испытаниях должна обеспечиваться в соответствии с действующими "Правилами техники безопасности при эксплуатации электроустановок потребителем", утвержденными Госэнергонадзором.
Приложение 1
Справочное
Пример определения числа измерений
1. Необходимое число измерений (n) вычисляют по формуле
 | |
| 460 × 189 пикс. Открыть в новом окне | |
2. Значение дисперсии случайной величины вычисляют по формуле
 | |
| 618 × 178 пикс. Открыть в новом окне | |
3. Значение критерия Стьюдента (t) при различных доверительных вероятностях табулированы и приведены в табл. 1.
Таблица 1
 | |
| 651 × 278 пикс. Открыть в новом окне | |
4. В качестве примера вычислим число параллельных измерений при оценке твердости покрытия по ГОСТ 5233-89 на основе эмали МЛ-12. Результаты измерений приведены в табл. 2.
5. Для первой выборки оценку математического ожидания вычисляют по формуле
 | |
| 316 × 89 пикс. Открыть в новом окне | |
дисперсию по формуле
 | |
| 468 × 63 пикс. Открыть в новом окне | |
Таблица 2
 | |
| 923 × 420 пикс. Открыть в новом окне | |
6. Для второй выборки оценку математического ожидания вычисляют по формуле
 | |
| 252 × 82 пикс. Открыть в новом окне | |
дисперсию по формуле
 | |
| 452 × 56 пикс. Открыть в новом окне | |
7. Среднее арифметическое заданных оценок дисперсии равно
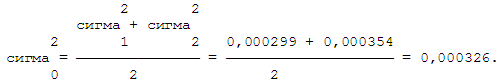 | |
| 498 × 84 пикс. Открыть в новом окне | |
8. Твердость покрытия в данном примере должна быть вычислена с точностью дельта = 0,015 и доверительной вероятностью Р = 0,95.
9. По табл. 1 находят значение критерия Стьюдента (t) при
доверительной вероятности  , равной 0,475.
, равной 0,475.
10. Число параллельных определений равно
 | |
| 247 × 87 пикс. Открыть в новом окне | |
После округления получаем n = 6.
Приложение 2
Справочное
Пример расчета температуры сушки покрытия изделия
1. Требуется определить температуру сушки покрытия в терморадиационной сушильной установке при продолжительности сушки 15 мин. Толщина стенок изделия 6 мм, материал - сталь, удельная теплоемкость материала 490 Дж/(кг x °С), плотность - 7800 кг/м3.
1.1. В соответствии с п. 5.3 покрытие образца сушат 15 мин при температуре 100°С.
1.2. По формуле п. 5.1 вычисляют коэффициент теплообмена при сушке покрытия образца толщиной 1 мм
 | |
| 365 × 65 пикс. Открыть в новом окне | |
1.3. По формуле п. 5.5 вычисляют значение обобщенного безразмерного коэффициента при сушке покрытия образца
 | |
| 264 × 61 пикс. Открыть в новом окне | |
