Ведомственные строительные нормы ВСН 51-88"Инструкция по уширению автодорожных мостов и путепроводов"(утв. Минавтодором РСФСР 26 июля 1988 г.) стр. 19

где N - число корреспондирующих пунктов; - объем перевозок по i-й корреспондирующей связи; , - соответственно абсцисса и ордината i-го корреспондирующего пункта.

1.5. Оптимальные объемы работ по уширению мостов первой группы определяют на основе локального подхода, предусматривающего рассмотрение вариантов развития габаритов мостов во времени; для второй группы мостов - на основе системного подхода, базирующегося на комплексном анализе условий функционирования всей совокупности мостов во времени и пространстве.

2. Определение оптимальных объемов работ по уширению мостов и очередности их выполнения для I группы сооружений

2.1. В качестве критерия при определении оптимальных размеров уширения и сроков реконструкции мостов следует принимать показатель приведенных затрат на реконструкцию сооружений и осуществление транспортного процесса в районе их тяготения. Учитывается многостадийность работ по уширению.

2.2. Целесообразность многостадийного уширения устанавливается после определения возможного срока службы сооружения до его полного физического износа, определения перспективной интенсивности движения и построения графика ее изменения в течение срока службы сооружения.

На графике роста интенсивности движения отмечают такие ее значения, которые в соответствии с существующими нормами являются нижними границами интенсивности для различных категорий дорог.

Если такая граница одна, то целесообразно одностадийное уширение при количестве граничных значений, равном двум и более, необходима проверка на стадийную реконструкцию.

2.3. При одностадийной реконструкции размер уширения определяется необходимостью увеличения габарита до следующего по величине. При этом оптимальный срок реконструкции моста определяют из выражения для приведенных затрат:

240 × 70 пикс.     Открыть в новом окне

, (1)

где C(t) - транспортно-эксплуатационные расходы в i-м году эксплуатации моста, тыс. руб.; - срок эксплуатации моста до уширения (год реконструкции) ( ); - срок службы моста, лет.

2.4. При возможности многостадийной реконструкции моста следует рассматривать варианты и одностадийного уширения. При этом принимают, что реконструкция первой стадии уширения осуществляется в данный момент, а срок проведения реконструкции 2-й и последующих стадий определяется расчетным путем. Наилучший вариант определяют по минимуму приведенных затрат:

250 × 73 пикс.     Открыть в новом окне

320 × 73 пикс.     Открыть в новом окне

,

где , , ... - единовременные затраты, связанные с реконструкцией моста соответственно 1-й, 2-й и Q-й стадии при i-м размере его уширения, тыс. руб.; - снижение транспортно-эксплуатационных затрат в t-м году эксплуатации моста в результате его уширения, тыс. руб.;

, , ..., - срок проведения реконструкции (уширения) моста 2-й и последующих стадий; Q - число стадий реконструкции (уширения) моста в период его эксплуатации.

Реализация целевой функции (2) может осуществляться вручную и по стандартной программе на ЭВМ.

2.5. При ручном методе расчета реализацию целевой функции осуществляют на основе построения функциональной модели динамического программирования, которая является графическим отображением моделируемого процесса (см. рисунок).

1915 × 1230 пикс.     Открыть в новом окне

Функциональную модель строят в прямоугольной системе координат, где на оси абсцисс (временной шкале) откладывают срок эксплуатации мостового сооружения; на оси ординат N выделяют существующий габарит моста и возможные варианты его развития в виде нескольких уровней (римские цифры), соответствующих типовой классификации габаритов мостов. На этой же оси фиксируют значения интенсивности движения, соответствующие каждому уровню функциональной модели.

На временной шкале выделяют отрезок n, характеризующий время эксплуатации моста с существующим габаритом до момента, соответствующего нижнему граничному значению интенсивности движения для большего габарита. Оставшийся период времени делят на несколько равных интервалов d. При этом допускается, что лишь в начале каждого интервала может приниматься решение о реконструкции моста с целью последующего увеличения его габарита.

Через точки деления оси абсцисс и ординат проводят соответственно вертикальные и горизонтальные сплошные линии; через точки, характеризующие центры интервалов оси абсцисс, - штриховые вертикальные линии. Точки пересечения штриховых вертикальных линий с горизонтальными (узлы функциональной модели) в получаемой решетке нумеруют, как показано на рисунке.

Начало координат (точку 0) соединяют наклонными стрелками с узлами функциональной модели, расположенными правее и выше. Эти стрелки имитируют затраты первой стадии реконструкции при уширении мостов до габаритов, соответствующих каждому уровню функциональной модели.

Отрезки горизонтальных линий от узлов до конца первого временного интервала заменяют горизонтальными стрелками, имитирующими транспортно-эксплуатационные затраты (или их снижение в результате реконструкции моста) в период эксплуатации сооружения, равный отрезку времени n.

Аналогично наклонными стрелками фиксируются затраты на реализацию рассматриваемых вариантов 2-й и последующих стадий реконструкции, осуществляемых в моменты соответственно , а горизонтальными стрелками - транспортно-эксплуатационные затраты (или их снижение) после проведения существующих реконструкций за отрезки времени d.

Маркировка наклонных стрелок полученной функциональной модели осуществляется показателями , характеризующими единовременные затраты и реконструкцию мостового перехода и рассматриваемые моменты времени с учетом коэффициентов дисконтирования . Верхние индексы при этих показателях указывают на исходную величину габарита моста (до очередной реконструкции) и последующий вариант его развития в результате реконструкции.

Горизонтальные стрелки функциональной модели маркируют размером суммарных транспортно-эксплуатационных затрат или суммарными размерами их снижения , связанными с осуществлением транспортного процесса через мостовой переход в периоды его эксплуатации между рассматриваемыми вариантами реконструкции. Верхний индекс при этих показателях указывает на вариант развития габарита моста, для которого рассчитывают транспортно-эксплуатационные затраты (или их снижение по сравнению с существующим габаритом моста).

При использовании функциональной модели решение задачи определения оптимальных размеров уширения и сроков реконструкции сводится к отысканию на сетевой диаграмме траектории (в направлении стрелок), обладающей минимальной суммой оценок, которыми помечены стрелки функциональной модели от точки 0 к линии АБ.

3. Определение оптимальных объемов работ по уширению мостов и очередности их выполнения для II группы сооружений

3.1. Используется следующая экономическая постановка задачи.

На водной преграде (водных преградах) известно местоположение одного или нескольких постоянных мостов (на разных дорогах) с недостаточной пропускной способностью, которые связаны с другими постоянными и временными мостовыми переходами дорожной сетью. Известны: количество корреспондирующих пунктов, связанных между собой посредством искусственных сооружений, расстояния перевозок между ними и интенсивность движения по корреспондирующим пунктам района тяготения мостов на исходный год и перспективу.

В результате решения задачи устанавливают:

оптимальные объемы работ (в ) по уширению существующих мостовых сооружений и строительству новых мостов по каждому году рассматриваемого планового периода;

последовательность выполнения во времени объемов работ по реконструкции и строительству сооружений;

интенсивность между всеми корреспондирующими пунктами, обеспечивающую рациональную маршрутизацию перевозок в районе тяготения искусственных сооружений.

3.2. При принятом критерии оптимальности целевая функция поставленной задачи описывается следующим образом:

566 × 126 пикс.     Открыть в новом окне

287 × 44 пикс.     Открыть в новом окне

,

где L, К - количество корреспондирующих пунктов, расположенных соответственно с левой и правой стороны водной преграды; l, k - номер корреспондирующего пункта соответственно с левой и правой стороны водной преграды (t = 1, 2,..., L), (k = 1, 2,..., К); n - количество постоянных и временных мостовых переходов в рассматриваемом районе; i - номер местоположения мостового перехода (t = 1, 2,..., n); T - продолжительность планового периода, годы; t - номер года планового периода (t = 1, 2,..., T); - количество вариантов габарита проезжей части i-го моста; - номер варианта габарита проезжей части i-го моста (р = 1, 2, ..., р), при p = 1 габарит моста равен 0; - затраты на строительство или реконструкцию моста в расчете на 1 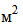его площади в i-м пункте при -м варианте его габарита; - коэффициент пропорциональности, характеризующий отношение между габаритом моста и его пропускной способностью (интенсивностью движения), (авт./сут); - пропускная способность моста (интенсивность движения в i-м пункте при 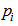-м варианте его габарита в году t), авт./сут; - переменная, выражающая требование целочисленности в формальной формулировке задачи и принимающая значения 0 или 1 ( означает, что данный вариант габарита моста входит в оптимальный план; характеризует такое положение, когда в i-й точке размещения дислоцирован мост на с -м вариантом габарита), ; - средняя грузоподъемность автомобилей в потоке, т; - себестоимость автомобильных перевозок между пунктами l и k через i-й мост в расчете на 1 ; - интенсивность движения автомобилей между пунктами l и k через i-й мост в год t, авт./сут; - интенсивность движения автомобилей между пунктами k и l через i-й мост в год t, авт./сут; 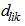- расстояние перевозок между пунктами l и k через i-й мост, км; - нормативный коэффициент экономической эффективности ( ).

3.3. Для решения задачи развития и размещения сети мостов на автомобильных дорогах в принятой постановке должны вводиться следующие ограничения:

1) пропускная способность (габарит) i-го моста должна быть не меньше имеющейся интенсивности движения:

224 × 73 пикс.     Открыть в новом окне

, ; ;

2) искомая суммарная пропускная способность мостов не должна быть меньше имеющейся:

239 × 79 пикс.     Открыть в новом окне

; ;

3) пропускная способность каждого существующего моста должна быть не меньше имеющейся:

; ; ,

где j - номер существующих постоянных мостов (j=1, 2,..., J); J - количество существующих мостов ( ); I - возможные точки размещения мостов ( );

4) суммарная интенсивность движения от i-х пунктов до k-го пункта через все мосты должна обеспечивать реализацию всех транспортных потоков, выходящих из пунктов l и входящих в пункт k:

; ; ;

5) интенсивность движения от k-го в i-е пункты должна обеспечивать реализацию всех транспортных потоков, выходящих из пункта k и входящих в пункты l:

; ; ;